Stefan H
- 3
- 0
- TL;DR Summary
- Solving Laplace's equation for magnetic potentials inside and outside a ferromagnetic wire with specific boundary conditions. Help needed in understanding how to obtain the solution.
Hello everybody,
Currently I am doing my master's thesis and I've encountered a physics problem which is very difficult for me to solve. The problem I have is finding equations for the magnetic scalar potential inside and outside a ferromagnetic wire for specific boundary conditions.
Explanation of the problem:
A ferromagnetic wire is located in an external magnetic field. This means there is a magnetic potential inside and outside of the wire. I want to find specific solutions on the surface of the wire (r=a).

My solution approach was to first solve Laplace's equation for polar coordinates for both magnetic potentials:
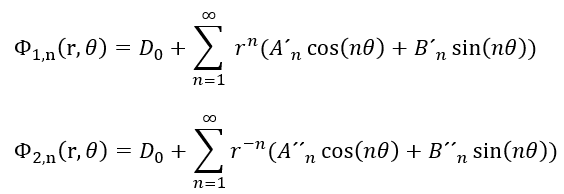
Now I want to find an expression for both potentials on the surface of the wire to obtain this solution (According to Gerber: "Applied Magnetism", 1994):
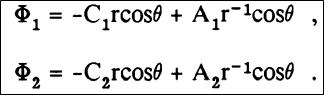
with the given boundary conditions:
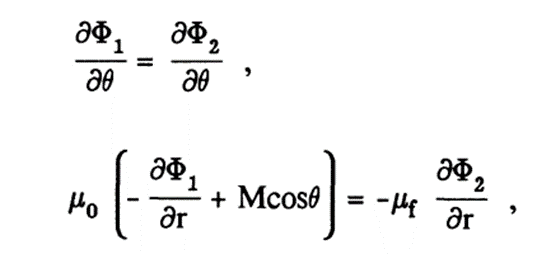
The next goal would be to determine the constants C1, A1, C2 and A2. However, I really don't get how Gerber came to this type of solution. He only mentioned to use Laplace's equation and the boundary conditions with quote: "linear combination of cylindrical harmonics" to get his solution.
My overall goal is to understand his approach for this kind of problem, so I can apply it to a different geometry. It would be very nice if anybody here could help me out :)
Thanks in advance and happy Holidays,
Stefan
Currently I am doing my master's thesis and I've encountered a physics problem which is very difficult for me to solve. The problem I have is finding equations for the magnetic scalar potential inside and outside a ferromagnetic wire for specific boundary conditions.
Explanation of the problem:
A ferromagnetic wire is located in an external magnetic field. This means there is a magnetic potential inside and outside of the wire. I want to find specific solutions on the surface of the wire (r=a).
My solution approach was to first solve Laplace's equation for polar coordinates for both magnetic potentials:
Now I want to find an expression for both potentials on the surface of the wire to obtain this solution (According to Gerber: "Applied Magnetism", 1994):
with the given boundary conditions:
The next goal would be to determine the constants C1, A1, C2 and A2. However, I really don't get how Gerber came to this type of solution. He only mentioned to use Laplace's equation and the boundary conditions with quote: "linear combination of cylindrical harmonics" to get his solution.
My overall goal is to understand his approach for this kind of problem, so I can apply it to a different geometry. It would be very nice if anybody here could help me out :)
Thanks in advance and happy Holidays,
Stefan
Last edited: