Solving Limit: x^2->∞, Why is Limit -1?

[Yankel]

Hello,

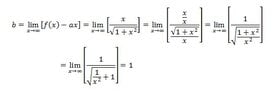
I have a problem with the attached limit. The problem is, that according to my calculations when x -> infinity, the limit is 1, which is fine, but what happens when x --> - infinity... ?

x is squared, so I think it should not matter, and the limit should remain 1, however, the correct answer is -1, and I just don't understand why or what I did wrong in my solution. An assistance will be appreciated !

View attachment 526

 

[Jameson]

Interesting question :) This isn't a rigorous argument but I think it should be sufficient.

I think it has to do with moving a variable in and out of the square root. $x \ne \sqrt{x^2}$ if $x<0$.

Take a look at [math]\sqrt{x^2+1}[/math]. Another way to manipulate this algebraically is to simply factor out an $x^2$ term like so:

[math]\sqrt{x^2 \left(1+ \frac{1}{x^2} \right)}=\sqrt{x^2} \sqrt{\left(1+ \frac{1}{x^2} \right)}[/math].

When simplifying $\sqrt{x^2}$ it's best to be careful and write it as $|x|$, which is what I think is appropriate now.

As before the limit of the [math]1+\frac{1}{x^2}[/math] part tends to 1, so what's remaining is [math]\frac{x}{|x|}[/math]. Since x is on the negative side of the number line in order to drop the absolute value bars we add a negative sign. That leaves us with [math]\frac{x}{|x|}=\frac{x}{-x}=-1[/math], where $x<0$.

 

[Deveno]

beware the square (it's not a 1-1 operation)!

not just being silly...

at one point you square x, and put it under the radical.

well, squaring a negative number ALWAYS gives you a positive number, so you've just changed the sign of your expression without realizing it.

what is wrong with the following proof:

a = -b
a/b = -1
(a/b)² = 1
a/b = √1 = 1
a = b ?

 

[Yankel]

Now I understand my mistake...thanks !
(Yes)