Solving Linearized EFE for Newtonian Potential Under Lorentz Gauge

[Arman777]

Under the Lorentz Gauge the Einstein Field Equations are given as

$$G^{\alpha \beta} = -\frac{1}{2}\square \bar{h}^{\alpha \beta}$$

Then the linearized EFE becomes,

$$\square \bar{h}^{\mu\nu} = -16 \pi T^{\mu\nu}$$

For the later parts, I ll share pictures from the book

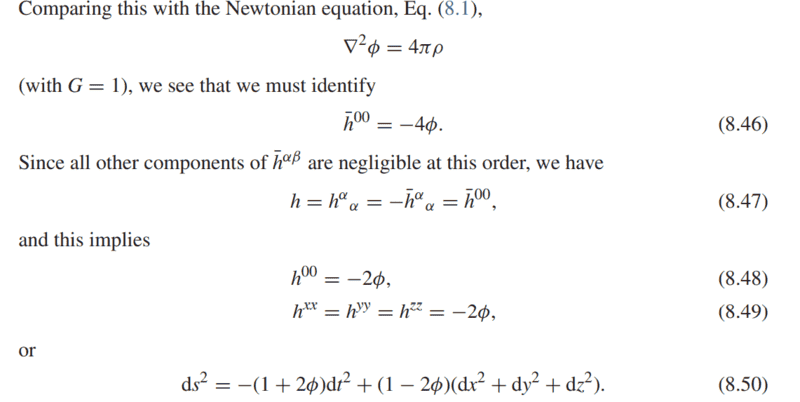I have couple of questions

1) I did not understand how the $\square$ becomes $\nabla^2$ for this case.

2) I did not understand equation 8.47 at all.

3) I also did not understand 8.49. Since he only defined $$\nabla^2\bar(h)^{0 0} = -16 \pi \rho$$.

Is there also terms like $\nabla^2\bar(h)^{xx} = -16 \pi \rho$, $\nabla^2\bar(h)^{yy} = -16 \pi \rho$ and $\nabla^2\bar(h)^{zz} = -16 \pi \rho$ ?

This might be helpful for you guys

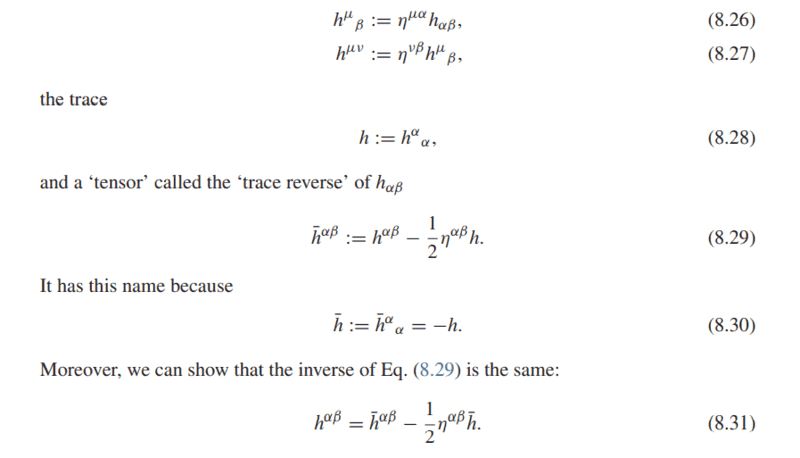
Please help. Thanks

For instance, by using 8.31 and 8.46 I can write,

$$h^{0 0} = -4\phi - \frac{1}{2} (-1) \bar{h}$$ but what is $\bar{h}$ here ?

If we only know (8.45), how can we calculate $h^{xx}$ ?

 

[Orodruin]

1) The argument is that $\partial_t$ is of order $v \partial_x$. Since $v\ll 1$, the $\partial_t$ terms are negligible.

2) This is just computing the trace of $h$. First step is the definition of the trace. Second step is using that $\bar h$ is the trace-reversed perturbation (take the trace of the definition of $\bar h_{ab}$). Last step is using that the 00 component is assumed to completely dominate $\bar h$.

3) No. The entire argumentation is based on the 00 component of the stress energy tensor dominating and all other terms therefore being negligible.

 

[Arman777]

1) The argument is that $\partial_t$ is of order $v \partial_x$. Since $v\ll 1$, the $\partial_t$ terms are negligible.

2) This is just computing the trace of $h$. First step is the definition of the trace. Second step is using that $\bar h$ is the trace-reversed perturbation (take the trace of the definition of $\bar h_{ab}$). Last step is using that the 00 component is assumed to completely dominate $\bar h$.

3) No. The entire argumentation is based on the 00 component of the stress energy tensor dominating and all other terms therefore being negligible.

Thanks for your answer.

1) I understand this one

2-3) So you mean $\bar{h}^{00} \gg \bar{h}^{11}, \bar{h}^{22} , \bar{h}^{33}$ ?

If that's the case, then how can we calculate $h^{xx}, h^{yy}$ and $h^{zz}$ ?

 

[Arman777]

Okay, solved it. Nvm