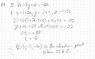Solving Lines & Planes Homework Statement: See 1st Figure

[jegues]

Homework Statement

See first figure.

Homework Equations

N/A

The Attempt at a Solution

I think I got part a down(See second figure) but I'm confused as to how to approach part b.

If it has to be parallel to line $$l$$ then its going to be in the same direction as $$l$$.

In other words, if $$\vec{u}$$ is the vector:

$$\vec{u} = <2,1,5>$$

Then the plane will be in the direction of $$\vec{u}$$.(Sorry if that sounds weird, I can't think of any other way to say it :shy:)

What property do I need to fufill in order to have my simplified equation of the plane through the point $$P(1,1,1)$$ such that it is perpendicular to the plane $$\Pi$$?

When I read this I automatically think about the dot product of two vectors,

$$\vec{P}\cdot\vec{Q} = |\vec{P}||\vec{Q}|cos(\theta)$$

But since they are perpendicular,

$$\vec{P}\cdot\vec{Q} = 0$$

Any suggestions?

 

[Raskolnikov]

The typical equation for a plane is of the form

$$\vec{n} \cdot \vec{P_0 P_1} = 0,$$

where n is a normal vector to the plane and P_0 P_1 is the vector from two points on the plane.

(Aside: can you figure out why this is always true? think of the properties of the dot product and the geometric relation between a vector on the plane and a normal vector to the plane.)

Let n = <a, b, c>. Now, if we know 1 point, P(x_0, y_0, z_0) on the plane, we can rewrite this as:

$$a(x - x_0) + b(y - y_0) + c(z - z_0) = 0.$$Alright, now for your problem specifically. We want our new plane to be perpendicular to the old plane and parallel to the given line. In other words, we want our new plane to contain both the normal vector of the old plane and $$\vec{u}.$$ But our general equation of a plane has coefficients a,b,c that make up a normal vector to the plane. How should we find a normal vector to our new plane when we know two vectors that lie on the plane?

By the way, how are you teaching all this to yourself? It seems you're running into many questions. I'd find a good textbook and just read through it carefully if I were you. Personally, I used Calculus, 5e by James Stewart. I liked it, but there are plenty of other good textbooks available. Just don't try to skim through this material by yourself. Actually sit down, read, and take notes in the textbook.

 

[Dick]

The normal vector of the second plane should be perpendicular to the tangent of l, if it's to be parallel to l, right? And if the second plane is perpendicular to first plane, it's normal vector should be perpendicular to the normal of the first plane, again right? I would say you have two given vectors and you want to find a vector normal to both of them. Sounds like a job for the cross product.

 

[jegues]

Aside: can you figure out why this is always true? think of the properties of the dot product and the geometric relation between a vector on the plane and a normal vector to the plane.

Because the normal of the plane is going to be perpendicular to any vector that lies in the plane. Since the dot product is defined as,

$$\vec{n}\cdot \vec{P_0 P_1}= |\vec{n}||\vec{P_0 P_1}|cos\theta$$

Since $$\theta = 90^{o}$$,

$$\vec{n}\cdot \vec{P_0 P_1}= 0.$$

How should we find a normal vector to our new plane when we know two vectors that lie on the plane?

If the I denote the normal of the first plane as $$\vec{n_1}$$ then,

$$\vec{n_1} = <2, 2, 1>$$

Since both the vectors $$\vec{n_1}$$ and $$\vec{u}$$ lie in our plane, we can find the normal by evaluating the cross product of those two vectors.

So if we let $$\vec{n_2}$$ denote the normal of our new plane,

$$\vec{n_1}\times\vec{u} = \vec{n_2}$$.

Is this the correct approach?

 

[Dick]

Yes, the normal to the second plane is the cross product of the line tangent and the normal to the first plane. If that's what you mean by 'u'.

 

[jegues]

Okay I think I'm a little confused with some terminology here Dick.

Yes, the normal to the second plane is the cross product of the line tangent and the normal to the first plane.

When you say line tangent I'm not entirely sure what you mean.

The line $$l$$ described by the parametric equations in the question describe the line. We could write this line in vector format as follows,

$$l = <1, -3, 4> + <2, 1, 5>t$$

This describes a straight line in space correct? It starts at the point (1, -3, 4) and goes in the direction of the vector <2, 1, 5> multiplied by some constant t.

So how do you find the tangent of $$l$$ if the line itself is a straight line?

What am I misunderstanding?

 

[Dick]

Okay I think I'm a little confused with some terminology here Dick.



When you say line tangent I'm not entirely sure what you mean.

The line $$l$$ described by the parametric equations in the question describe the line. We could write this line in vector format as follows,

$$l = <1, -3, 4> + <2, 1, 5>t$$

This describes a straight line in space correct? So how do you find the tangent of $$l$$ if the line itself is a straight line?

What am I misunderstanding?

You aren't misunderstanding anything. What I mean by the tangent of the line is <2,1,5>. It's the 'direction vector' of the line. It's dl/dt. It's a vector that points along the direction of the line regardless of origin. I'm running out of synonyms here.

 

[jegues]

You aren't misunderstanding anything. What I mean by the tangent of the line is <2,1,5>. It's the 'direction vector' of the line. It's dl/dt. It's a vector that points along the direction of the line regardless of origin. I'm running out of synonyms here.

Haha, thanks again Dick. I seemed to have confused myself. It makes sense now!

 

[Raskolnikov]

l is a line that exists at specific points in R^3. We don't want to deal with a line with specific points, we want a vector (which has direction but isn't fixed). All we want is the general direction: the 'direction vector.'