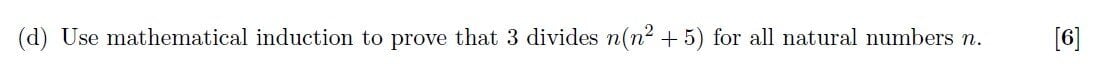- #1
delc1
- 9
- 0
Could anyone please help with this question regarding mathematical induction;
View attachment 2667
step by step procedure/ solution would be greatly appreciated. Thanks!
View attachment 2667
step by step procedure/ solution would be greatly appreciated. Thanks!