- #1
hav0c
- 58
- 0
Homework Statement
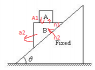
A block A of mass m is placed over a wedge B of same mass m. Assuming all surface to be smooth. The displacement of block A is 1 sec if the system is released from rest is :
Homework Equations
The Attempt at a Solution
i have made fbds and have the relations-
1. ma1=(g-N1)/m
2.N1cos θ+mg cosθ=N2
3.ma2=sinθ(mg+N1)
now I am stuck