- #1
sandpants
- 21
- 0
I have the following 2 problems to solve using Laplace.
1) x'' + 3x' +2x=e^(-t); with x=dx/dt=0 when t = 0
2) x'' - 2x' +10x=e^(2t); with x=0 and dx/dt=1 when t=0
Where x' is dx/dt and x'' is the second derivative against time.
My attempts:
1)Using laplace I get
s2X(s)-x(0)-x'(0)+3sX(s)-x(0)+2X(s)=1/(s+1)
with x(0)=0, x'(0)=0 then
X(s)=1 over (s+1)(s2+3s+2) which is 1/[(s+1)(s+1)(s+2)] or 1/[(s+1)2(s+2)]
Using partial fraction
1/[(s+1)2(s+2)]=A/(s+1)+B/(s+1)2+C/(s+2).
I'll avoid doing the calcs; I may have made a mistake here, but I checked multiple times and didnt find and error.
A=10/12, B=-1/6 and C=-1 so that, after doing inverse laplace
x(t)=5/6e-t-1/6t*e-t-e-2t
But here's the issue. With this, x(0)=/=0. It's -1/6. and dx(0)/dt=1. I can't figure out where I went wrong.
2)The laplace transform is
s2 X(s)-x(0)-x'(0)-2sX(s)-x(0)+10X(s)=1/(s-2)
with x'(0)=1 this rearranges to
X(s)(s2-2s+10)=1/(s-2)+1=(s-1)/(s-2)
X(s)=(s-1)/[(s-2)(s2-2s+10)]
This is where I helplessly run around in circles. The quadratic roots are complex, and whilst they discomfort me only slightly, the issue is that I cannot rearrange this into a suitable form where the inverse laplace can be done.
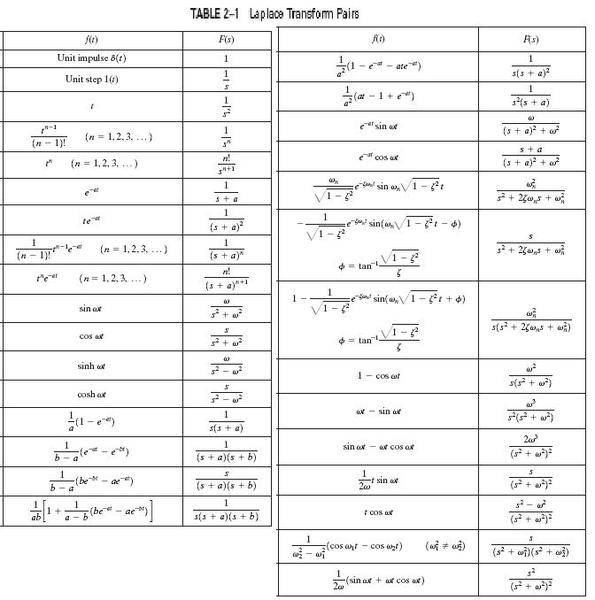
Taken from http://www.therationaltheorist.org/2009/11/fourier-analysis-and-odes.html
1) x'' + 3x' +2x=e^(-t); with x=dx/dt=0 when t = 0
2) x'' - 2x' +10x=e^(2t); with x=0 and dx/dt=1 when t=0
Where x' is dx/dt and x'' is the second derivative against time.
My attempts:
1)Using laplace I get
s2X(s)-x(0)-x'(0)+3sX(s)-x(0)+2X(s)=1/(s+1)
with x(0)=0, x'(0)=0 then
X(s)=1 over (s+1)(s2+3s+2) which is 1/[(s+1)(s+1)(s+2)] or 1/[(s+1)2(s+2)]
Using partial fraction
1/[(s+1)2(s+2)]=A/(s+1)+B/(s+1)2+C/(s+2).
I'll avoid doing the calcs; I may have made a mistake here, but I checked multiple times and didnt find and error.
A=10/12, B=-1/6 and C=-1 so that, after doing inverse laplace
x(t)=5/6e-t-1/6t*e-t-e-2t
But here's the issue. With this, x(0)=/=0. It's -1/6. and dx(0)/dt=1. I can't figure out where I went wrong.
2)The laplace transform is
s2 X(s)-x(0)-x'(0)-2sX(s)-x(0)+10X(s)=1/(s-2)
with x'(0)=1 this rearranges to
X(s)(s2-2s+10)=1/(s-2)+1=(s-1)/(s-2)
X(s)=(s-1)/[(s-2)(s2-2s+10)]
This is where I helplessly run around in circles. The quadratic roots are complex, and whilst they discomfort me only slightly, the issue is that I cannot rearrange this into a suitable form where the inverse laplace can be done.
Taken from http://www.therationaltheorist.org/2009/11/fourier-analysis-and-odes.html