Solving Paul Tipler's Challenging Physics Problem

[franz32]

Hello. I was trying to solve this challenging problem from oneof the questions made by Paul Tipler... (he's tough)

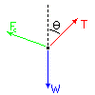
Suppose that the two masses that are suspended from a common point by threads of length L, are not equal. One mass is 0.01 kg and the other is 0.02 kg. The charges on the two masses are 2 and 1 microcoulomb respectively. Determine the angle that each of the strings supporting the masses makes with the vertical.

(p.687 #90 - Physics for scientists and engineers: 4th edition)

 

[quantumdude]

Draw the free body diagram with the charges suspended at some unspecified angle θ Then put in all the forces (gravity, electrostatic, and tension). Since you have 2 dimensions, Newton's second law will yield 2 equations. Happily, you only have 2 unknowns (the angle and the tension).

 

[franz32]

Hello Sir Tom

Hello.

So, I'll eventually reach for 2 unknowns? Hmmm, are the
angles must be different from each other?

 

[FZ+]

Yes, the two angles are different, as the masses and hence weight forces acting on the two bodies are different.

 

[franz32]

How should I do it?

Hello

What I did to the problem is that I made two separate free body diagrams involving the two masses. For each diagram, say on the left portion of the main figure, the F is pointing on the left, the W(1) downward and the Tension slant upward to the right. Then, I got all the summation of forces with respect to x and y axes.

Next, considering the 2nd free body diagram (right side), I did the same thing as what I've done from above. Am I doing right?

 

[Spectre5]

break the tension into its x and y components

the angles are different

remember that both x parts of the tension have to be equal in magnitude and one is negative...and this magnitude must equal the repulsive force of the charges

edit: and the y parts of the tension are equal to the weight of each sphere (hence the reason your tensions will be different)

 

[turin]

I don't think that the tension is so important. It looks like it would be better to introduce a constraint (the lengths of the cables = L). Then, transform into polar coordinates.

EDIT:
OK, it looks like it will work well if you transform into polar coordinates with the two generalized coordinates being the angle that each cable makes with the verticle (the trick is to know what to use for your coordinates). Express your potential energies in terms of these coordinates and minimize.

Originally posted by Spectre5
... both x parts of the tension have to be equal in magnitude ...

Are you sure about this? I was thinking that this assumption cannot be made. Can you elaborate/tell us why this is so?

EDIT:
Now I think I see why. I am drawing the free body diagrams now. Well, I'll solve the problem to see if the x tensions are in fact equal and then post my findings. I agree with you now. Even without the free body diagram or a solution, I should have realized (as I suppose you did) that the only external forces acting on the system are the tensions and gravity, and since gravity is a net y force, the net tension should be a net y force.

 

[Spectre5]

Well, if the balls are no longer moving (as they are not), then the sumation of forces in the x direction must be equal, from Newton's laws.

All that is going in the x direction (assuming you have your x and y systems setup the same as I would do it), then in the x direction, you would only have a tension vector component in the x direction and the repulsive force.

Since the repulsive forces is equal on both of the spheres, the x component of the tension must also be equal if the system is in static equilibrium

 

[turin]

Originally posted by Spectre5
... (assuming you have your x and y systems setup the same as I would do it), then in the x direction, you would only have a tension vector component in the x direction and the repulsive force.

Did you allign your x-axis with the cable?

Originally posted by Spectre5
Since the repulsive forces is equal on both of the spheres, the x component of the tension must also be equal if the system is in static equilibrium

I don't follow this. The way I have it, all three forces play a nontrivial role (though I treat the cable as a constraint instead of a tension, so I have two forces). I am attaching a free body diagram for one of the masses. Tell me if I am misinterpretting the problem.




EDIT:
Oh, wait, I see what you mean now (I think). For some reason I've been very confused by the wording today. Disregard everything that I wrote in this post.




All right, this is now bothering me. I can solve neither approach (minimization of energy nor force balancing). I wind up getting some hairy trig relationships. I feel pathetic. Does anyone have the solution (how to get around the trig)?