- #1
dandirom
- 9
- 0
Hi there,
I'd like some help with the formulas of these following problems. I just need some tips on how to go about answering them -- I'd like to solve them on my own though.
1.
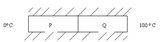
Two rods of equal lengths and cross-sectional areas but of different materials are placed in thermal contact as shown in Figure 2. The thermal conductivity of Q is half that of P. The outer end of P
is at 0 C and that of Q is at 100 C.
What is the temperature of the interface at steady state?
2.
In two experiments with a continuous flow calorimeter to determine the specific heat capacity of a liquid, an input power of 60 W produced a rise of 10 K in the liquid. When the power was doubled, the same temperature rise was achieved by making the rate of flow of liquid three times faster. The power lost to the surroundings in each case was?
3.
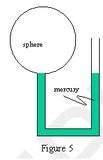
A glass sphere of volume 7 l contains air at 27C and is connected to a pipe filled with mercury as shown in Figure 5 below. At the start, the mercury meniscus is level with the bottom of the sphere on both arms of the pipe. The air in the sphere is now heated and the mercury level on the right arm rises 5 mm. If the cross sectional area of the pipe is 10 cm2, what is the new temperature of the air (in C)?
4.
The distance between the double slits to the screen is 3.0 m. The slit separation is 0.2 mm, and the wavelength of incident light is 633 nm.
(i) Determine the angular displacement of the third order minima.
(ii) Determine the fringe width of the interference pattern observed on the
screen.
(iii) Estimate the theoretical maximum number of bright fringes that can be observed.
(iv) If the widths of the slits are assumed to be infinitely small and y is the distance from the central maxima on the screen, sketch a clearly labelled graph to show the variation of the intensity of the fringe pattern with y. The intensity of the waves from each slit is I0. Express the intensity in terms of I0.
(v) The slit S1 is now covered with a filter such that the light emerging from S1 is reduced by half in amplitude. Sketch on the same graph for part (iv), the new intensity pattern you would expect to observe. Label your graphs clearly.
I'd like some help with the formulas of these following problems. I just need some tips on how to go about answering them -- I'd like to solve them on my own though.
1.
Two rods of equal lengths and cross-sectional areas but of different materials are placed in thermal contact as shown in Figure 2. The thermal conductivity of Q is half that of P. The outer end of P
is at 0 C and that of Q is at 100 C.
What is the temperature of the interface at steady state?
2.
In two experiments with a continuous flow calorimeter to determine the specific heat capacity of a liquid, an input power of 60 W produced a rise of 10 K in the liquid. When the power was doubled, the same temperature rise was achieved by making the rate of flow of liquid three times faster. The power lost to the surroundings in each case was?
3.
A glass sphere of volume 7 l contains air at 27C and is connected to a pipe filled with mercury as shown in Figure 5 below. At the start, the mercury meniscus is level with the bottom of the sphere on both arms of the pipe. The air in the sphere is now heated and the mercury level on the right arm rises 5 mm. If the cross sectional area of the pipe is 10 cm2, what is the new temperature of the air (in C)?
4.
The distance between the double slits to the screen is 3.0 m. The slit separation is 0.2 mm, and the wavelength of incident light is 633 nm.
(i) Determine the angular displacement of the third order minima.
(ii) Determine the fringe width of the interference pattern observed on the
screen.
(iii) Estimate the theoretical maximum number of bright fringes that can be observed.
(iv) If the widths of the slits are assumed to be infinitely small and y is the distance from the central maxima on the screen, sketch a clearly labelled graph to show the variation of the intensity of the fringe pattern with y. The intensity of the waves from each slit is I0. Express the intensity in terms of I0.
(v) The slit S1 is now covered with a filter such that the light emerging from S1 is reduced by half in amplitude. Sketch on the same graph for part (iv), the new intensity pattern you would expect to observe. Label your graphs clearly.