Solving Problem 6c: Time Taken from A to B and B to C

[chwala]

Homework Statement

see attached.

Relevant Equations

Relative Velocity

My interest is only on Example 6; part c only, see the problem below and the solution from textbook.

is the time calculated correctly? I thought we need to use the approach shown below; my thoughts, but of course i may be missing something here, The time taken from points $A$ to $B$ is the same as the time taken from point $B$ to $C$, i used the thinking of resultant distance divide by resultant velocity.

 

[Mark44]

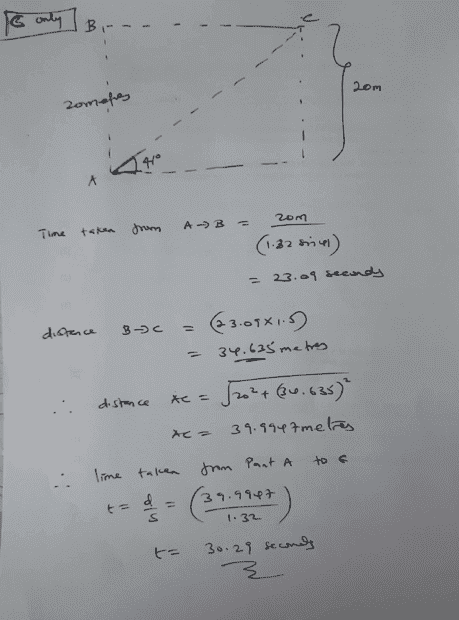
is the time calculated correctly?

The time shown in Ex. 6 looks fine to me.

I thought we need to use the approach shown below; my thoughts, but of course i may be missing something here,

Your approach doesn't seem to be correct. The major difference between your work and the work shown in the example is that you don't seem to be taking into account the swimmer's speed in still water vs. the swimmer's speed in the moving river. The worked example does take this difference into account.

The time taken from points A to B is the same as the time taken from point B to C, i used the thinking of resultant distance divide by resultant velocity.

Again, you are not taking into account that the water in the river is moving, and in so doing is making the swimmer's speed greater than it would be if he were swimming in a lake (where the water is not moving).

 

[chwala]

The time shown in Ex. 6 looks fine to me.

Your approach doesn't seem to be correct. The major difference between your work and the work shown in the example is that you don't seem to be taking into account the swimmer's speed in still water vs. the swimmer's speed in the moving river. The worked example does take this difference into account.

Again, you are not taking into account that the water in the river is moving, and in so doing is making the swimmer's speed greater than it would be if he were swimming in a lake (where the water is not moving).

I considered the speeds in still water and moving water, ...that's how we ended up with resultant velocity being equal to $1.32$m/s. You can see that i attempted to use it on my last part of my working i.e in finding;
$time$= $\frac {distance}{resultant velocity}$.

On a different note, I can see that the resultant velocity was broken down into the two components, maybe the only thing that i need to understand is why they divided by sine...of course a quick guess is that sine takes into account the perpendiculor distance of the river bank (i.e the 20m).

 

[chwala]

Aaaargh Mark. I nailed it man!

On looking at the same problem, i was able to use a different approach to realize the desired result. That is;

I understand my approach better. One just needs to find the distance $BC$ as indicated on my sketch diagram. Bingo guys

 

[vela]

The easiest approach for the time is to note that the vertical (on the diagram) component of velocity comes only from the swimmer's velocity in still water. Since the vertical distance is 20 m, the time is
$$t = \frac{\Delta y}{v_y} = \frac{20.0~\rm m}{(1~{\rm m/s})\sin 60^\circ} = 23~\rm s.$$

 

[chwala]

The easiest approach for the time is to note that the vertical (on the diagram) component of velocity comes only from the swimmer's velocity in still water. Since the vertical distance is 20 m, the time is
$$t = \frac{\Delta y}{v_y} = \frac{20.0~\rm m}{(1~{\rm m/s})\sin 60^\circ} = 23~\rm s.$$

I get it now...thanks...you made it clear, thanks to you and Mark, what i can see is that we may use the right angle triangle for the swimmer's velocity in still water i.e in using the right angle triangle and trig. concepts knowledge we get,

$t$= $\frac {20}{1 × sin 60}$ = $\frac {20}{ 1.32 ×sin 41} = 23.09$ seconds ≈ $23$ seconds