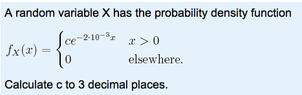Solving Random Variable Work: 0 to Infinity = 0.002?

[Uniman]

View attachment 432

Work done so far...

Integrating from 0 to infinity and equating it to 1, we get

(c/2*10^-3) = 1

c= 2/1000

=0.002

Is it correct?
http://www.chegg.com/homework-help/questions-and-answers/-q3136942#

 

[Sudharaka]

https://www.physicsforums.com/attachments/432

Work done so far...

Integrating from 0 to infinity and equating it to 1, we get

(c/2*10^-3) = 1

c= 2/1000

=0.002

Is it correct?
http://www.chegg.com/homework-help/questions-and-answers/-q3136942#

Hi Uniman, :)

Yes the method you have used is correct.

\[\int_{0}^{\infty}C\,\mbox{exp}\left(-\frac{2.1x}{1000}\right)dx=1\]

\[\Rightarrow C\left[-\frac{1000}{2.1}\mbox{exp}\left(-\frac{2.1x}{1000}\right)\right]^{\infty}_{0}=1\]

\[\Rightarrow \frac{1000}{2.1}C=1\]

\[\therefore C=\frac{2.1}{1000}=0.0021\]

Kind Regards,
Sudharaka.