Micheal_Leo
- 103
- 4
Hello
I have two equations given below and answer is also given solve by simultaneously
i am not sure how this happen
please guide thank you
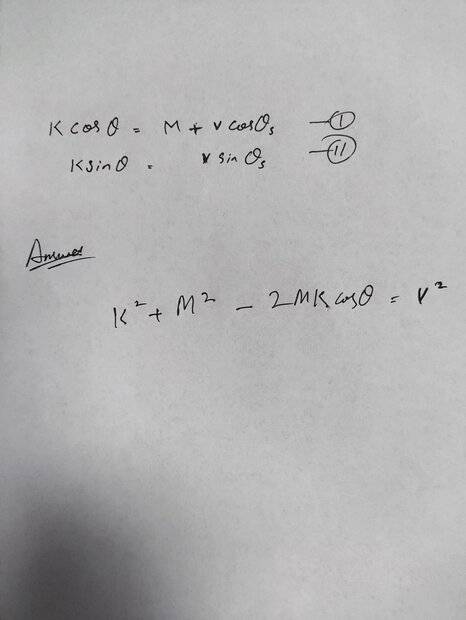
I have two equations given below and answer is also given solve by simultaneously
i am not sure how this happen
please guide thank you
Last edited by a moderator: