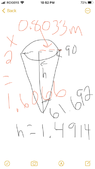PhysicsInept
- 9
- 1
Help please - okay so I have a question and struggling here.
I need to know the radius of the sphere and how much water it displaces.
One sphere inside an inverted cone
One sphere for which the maximum possible amount of water is displaced.
The problem is I’m only given the height of the cone and the semivertical angle Any idea what formula to use? I found some but none account for semivertical angle.
Thanks
I need to know the radius of the sphere and how much water it displaces.
One sphere inside an inverted cone
One sphere for which the maximum possible amount of water is displaced.
The problem is I’m only given the height of the cone and the semivertical angle Any idea what formula to use? I found some but none account for semivertical angle.
Thanks