Solving system of differential equations using matrix exponential

In summary, solving a system of differential equations using matrix exponential involves expressing the system in matrix form and utilizing the matrix exponential function to find the solution. The matrix exponential, denoted as \( e^{At} \), where \( A \) is the coefficient matrix, allows for the computation of the solution to the system by transforming the problem into a more manageable form. This method is particularly useful for linear systems, providing an efficient way to analyze the behavior of the system over time. The solution can be represented as \( \mathbf{x}(t) = e^{At} \mathbf{x}(0) \), where \( \mathbf{x}(0) \) is the initial condition vector.
  • #1
member 731016
Homework Statement
Please see below
Relevant Equations
Please see below
For this problem,
1715474953990.png

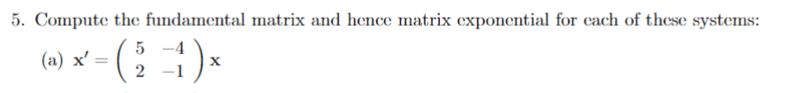
The solution is,
1715475028077.png

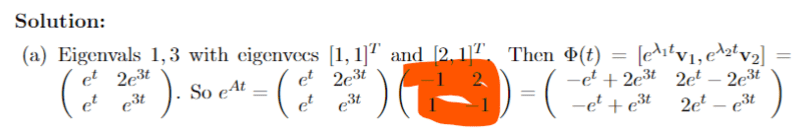
However, can someone please explain to me where they got the orange coefficient matrix from?It seems different to the original system of the form ##\vec x' = A\vec x## which is confusing me.

Thanks!
 

Attachments

  • 1715474985077.png
    1715474985077.png
    14.4 KB · Views: 39
Physics news on Phys.org
  • #2
This is all about transforming the original matrix A into it's Jordan normal form as the easy way to solve ##e^{At}## (the state transition matrix). But then you have to do the inverse transformation to get it back to the original basis. The reason you find the eigenvectors is to create the Jordan form, which, for simple systems is just a matrix with the e-values on the diagonal.

So, in your case the transform to the Jordan normal form uses the e-vector matrix ##H=
\begin{bmatrix}
1 & 2\\
1 & 1
\end{bmatrix}##
What is it's inverse ##H^{-1}## and how would you use it?

https://math24.net/method-matrix-exponential.html
https://sites.millersville.edu/bikenaga/linear-algebra/matrix-exponential/matrix-exponential.html

plus soooo many other versions of this problem on the web.
 
  • Love
Likes member 731016
  • #3
This is also an excellent video of ##e^{At}##.
 
  • Love
Likes member 731016
  • #4
Thank you for your replies @DaveE!

Do you please know why ##Φ'(t) = e^{At}Φ(0)## where ##Φ## is fundamental matrix?

Thanks!
 

FAQ: Solving system of differential equations using matrix exponential

What is the matrix exponential and why is it important in solving systems of differential equations?

The matrix exponential, denoted as exp(At) for a matrix A and time t, is a fundamental concept in linear algebra that extends the notion of the exponential function to matrices. It is crucial for solving systems of linear differential equations because it provides a way to express the solution of the system in terms of the initial conditions and the behavior of the system over time. Specifically, for a system described by the equation dx/dt = Ax, the solution can be written as x(t) = exp(At)x(0), where x(0) is the initial condition.

How do you compute the matrix exponential for a given matrix?

There are several methods to compute the matrix exponential, including the Taylor series expansion, diagonalization, and the use of the Jordan form. The Taylor series expansion is given by exp(A) = I + A + A²/2! + A³/3! + ... , where I is the identity matrix. If the matrix A can be diagonalized, exp(A) can be computed more easily using the formula exp(A) = PDP⁻¹, where D is a diagonal matrix of eigenvalues and P is the matrix of eigenvectors. For matrices that cannot be diagonalized, the Jordan form can be used to compute the exponential in a similar manner.

Can all systems of differential equations be solved using the matrix exponential?

Matrix exponentials can be used to solve linear systems of differential equations, specifically those of the form dx/dt = Ax, where A is a constant matrix. However, for nonlinear systems or systems with time-dependent coefficients, the matrix exponential method may not be applicable. In such cases, other techniques, such as numerical methods or qualitative analysis, may be necessary to find solutions.

What are the advantages of using the matrix exponential method over other methods?

The matrix exponential method offers several advantages for solving linear systems of differential equations. It provides an explicit formula for the solution, which can be computed efficiently, especially for large systems. Additionally, it allows for an easy understanding of the system's behavior in terms of its eigenvalues and eigenvectors, which can provide insights into stability and dynamics. The method is also versatile, as it can be applied to various initial conditions and can be extended to systems with constant coefficients.

How does the eigenvalue-eigenvector decomposition relate to the matrix exponential?

The eigenvalue-eigenvector decomposition plays a crucial role in simplifying the computation of the matrix exponential. When a matrix A can be expressed in the form A = PDP⁻¹, where D is a diagonal matrix containing the eigenvalues of A and P is the matrix of corresponding eigenvectors, the matrix exponential can be computed as exp(A

Similar threads

Fundamental matrix for complex linear DE system
Replies
4
Views
846
Fundamental matrix linear system equivalent to linear matrix system
Replies
2
Views
624
Relationship between autonomous system and related single equation
Replies
3
Views
1K
Solving a system of differential equations by fundamental matrix
Replies
8
Views
2K
Complex Eigenvalues of system of DE
Replies
3
Views
606
Solutions of first-order matrix differential equations
Replies
5
Views
1K
Solution for differential equation
Replies
2
Views
960
Solving system of differential equations using elimination method
Replies
10
Views
947
Proving stability of linear system equations
Replies
2
Views
725
Continue solutions of ODEs around the origin
Replies
2
Views
915

Hot Threads

Recent Insights

Back
Top