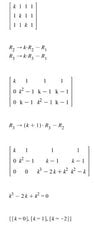- #1
Yankel
- 395
- 0
Hello
I have been trying to solve this system of equations, I need to find for which values of k the system has infinite number of solutions, no solution and a single solution.
I did some work, and found that for k=0 and k=1 there are infinite number of solutions and for k=-2 there is no solution.
However, for k=0 I ran this system on Maple and it found a single solution. What did I do wrong here ?
View attachment 308
thank you !
I have been trying to solve this system of equations, I need to find for which values of k the system has infinite number of solutions, no solution and a single solution.
I did some work, and found that for k=0 and k=1 there are infinite number of solutions and for k=-2 there is no solution.
However, for k=0 I ran this system on Maple and it found a single solution. What did I do wrong here ?
View attachment 308
thank you !