satu
- 3
- 0
- TL;DR Summary
- Methods to find solutions of system of PDEs
HI
HI! While trying to solve problem in Hydrodynamic stability I have got a system of Two Partial Diffential equations :
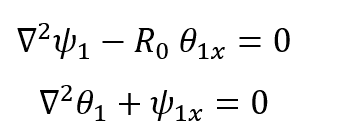
Can anyone help me to solve this analytically? Is there any general method to solve system of PDEs?
HI! While trying to solve problem in Hydrodynamic stability I have got a system of Two Partial Diffential equations :
Can anyone help me to solve this analytically? Is there any general method to solve system of PDEs?