Solving the Flocking Problem: Finding A,B,C Meeting Point

[chester20080]

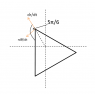
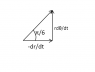
We have three masses (A,B,C), (all the same,m) that each one is on one vertex of an equilateral triangle of a side a.Each mass moves at a constant velocity u all the time.The rule for the motion of the masses is that they every one will always move towards the other in the way A->B->C->A.We have to find WHERE they will meet (our professor said that they will meet somewhere,as this can be proven,but we don't have to show that) and WHEN.The system is initially at rest with the initial positions I mentioned,with any two masses to have a distance a=edge and as soon as we let it free the masses start moving with u=constant (in magnitude) and according to that rule.
I can't find any equations to start from.Obviously if I could determine some direction vectors...But how?I mean what is the physics and the math behind such a phenomenon?Please help!

 

[tiny-tim]

hi chester20080!

how symmetrical is it?

what can you say about the positions at a general time t?

what can you say about the velocities at a general time t?

 

[chester20080]

If I could have these equastions about t,then I could answer.The question is how to find such equations.How can I translate into math the rule each body is heading to the other?As I imagine the masses will make something like a spiral and then they will meet.

 

[tiny-tim]

you don't need equations yet

just consider the symmetry​

 

[chester20080]

But how considering just the symmetry can I solve this?The symmetry is that every mass is far away from every other mass the same distance for every t,except for when they meet.As our professor said and intuitively,they will meet at the center of the triangle,but how can I prove this without any equations?

 

[tiny-tim]

But how considering just the symmetry can I solve this?The symmetry is that every mass is far away from every other mass the same distance for every t …

so the shape ABC at any time t is … ?

 

[chester20080]

An equilateral triangle of a side a'<a which decreases every time until they meet (a'=0).So...?

 

[tiny-tim]

An equilateral triangle of a side a'<a which decreases every time until they meet (a'=0).

yes

now how about the three velocities (at a general time t)?

 

[chester20080]

They will have the initial magnitude generally (u=constant) but their direction will change every time.

 

[tiny-tim]

yes they will all have the same magnitude, but how will their directions be related?

 

[chester20080]

The direction of the one will be towards the previous position of the other.

 

[tiny-tim]

but how will the direction of one be related to the direction of the others?

 

[chester20080]

Will it be direction1= -(direction2+direction3)?

 

[Chestermiller]

Will it be direction1= -(direction2+direction3)?

This is purely a geometry (kinematics) problem, and has nothing to do with physics. Consider using a coordinate system. Here are some possibilities:

(a) Cylindrical coordinates with the origin at one of the masses.
(b) Cartesian coordinates with the origin at one of the masses.
(c) Cylindrical coordinates with the origin at the center of the triangle (i.e., center of the inscribed and circumscribed circles)
(d) Cartesian coordinates with the origin at the center of the triangle.

If you had to choose, which one do you thing would be most convenient to use?

Chet

 

[chester20080]

As I am not very familiar with cylindrical coordinates,I would choose d),but I sense the right one is something with cylindrical...

 

[Chestermiller]

As I am not very familiar with cylindrical coordinates,I would choose d),but I sense the right one is something with cylindrical...

Would it be correct to say that you are currently studying cylindrical coordinates in your course? If not, where did this problem come from?

Chet

 

[chester20080]

Cylindrical coordinates we studied only once in analytic geometry and only the basics,the definition and the basic equations.Nothing else,no examples,no further details.This exercise is from the physics course and our professor told us that it is not a part of the course(no such thing will be in the exams),but gave us this problem nevertheless,just to keep those who are interested in action for the holidays.Who knows?

 

[chester20080]

So how do I proceed?

 

[tiny-tim]

suppose the velocity of one mass at time 0 is (u,0) …

what are the velocities of the other two masses? ​

(and what is the relative velocity of two of the masses?)

 

[Chestermiller]

So how do I proceed?

This problem can be set up in cartesian coordinates also. Let the locations of the three masses at time t be given by the coordinates (x1, y1), (x2, y2), and (x3, y3). What is the equation for a position vector from the origin drawn to each of these three points, in terms of the unit vectors in the x and y directions? What is the equation for the position vector from point 1 to point 2? From point 2 to point 3? From point 3 to point 1? In terms of the unit vectors in the x and y directions, what is the equation for a unit vector pointing from point 1 to point 2? From point 2 to point 3? From point 3 to point 1? Using this result, what is the vector velocity of point 1 relative to the origin? Of point 2 relative to the origin? Of point 3 relative to the origin?

Chet

 

[Tanya Sharma]

Hello Chet

I would like to do this problem.

This problem can be set up in cartesian coordinates also. Let the locations of the three masses at time t be given by the coordinates (x1, y1), (x2, y2), and (x3, y3).

What is the equation for a position vector from the origin drawn to each of these three points, in terms of the unit vectors in the x and y directions?

$$ \vec{r_1} = x_1\hat{i}+y_1\hat{j} $$

$$ \vec{r_2} = x_2\hat{i}+y_2\hat{j} $$

$$ \vec{r_3} = x_3\hat{i}+y_3\hat{j} $$

What is the equation for the position vector from point 1 to point 2? From point 2 to point 3? From point 3 to point 1?

$$ \vec{r_{21}} = (x_2-x_1)\hat{i}+(y_2-y_1)\hat{j} $$

$$ \vec{r_{32}} = (x_3-x_2)\hat{i}+(y_3-y_2)\hat{j} $$

$$ \vec{r_{13}} = (x_1-x_3)\hat{i}+(y_1-y_3)\hat{j} $$

In terms of the unit vectors in the x and y directions, what is the equation for a unit vector pointing from point 1 to point 2? From point 2 to point 3? From point 3 to point 1?

$$ \hat{r_{21}} =\frac{1}{\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}} (x_2-x_1)\hat{i}+(y_2-y_1)\hat{j} $$

$$ \hat{r_{32}} = \frac{1}{\sqrt{(x_3-x_2)^2+(y_3-y_2)^2}}(x_3-x_2)\hat{i}+(y_3-y_2)\hat{j} $$

$$ \hat{r_{13}} = \frac{1}{\sqrt{(x_1-x_3)^2+(y_1-y_3)^2}}(x_1-x_3)\hat{i}+(y_1-y_3)\hat{j} $$

Using this result, what is the vector velocity of point 1 relative to the origin? Of point 2 relative to the origin? Of point 3 relative to the origin?

$$ \vec{v_1} = \dot{x_1}\hat{i}+\dot{y_1}\hat{j} $$

$$ \vec{v_2} = \dot{x_2}\hat{i}+\dot{y_2}\hat{j} $$

$$ \vec{v_3} = \dot{x_3}\hat{i}+\dot{y_3}\hat{j} $$

Is it correct ?

If yes,what should be the next step ?

 

[Saitama]

Hello Tanya!

I suggest using polar coordinates for the problem. Can you write down a few equations for the motion of mass $m$?

To make things simpler, consider the origin at the centroid of equilateral triangle.

 

[Tanya Sharma]

I haven't worked much with polar coordinates but I will give a try .

I know a couple of things .

$$ \vec{r} = r\hat{r}$$
$$ \vec{v} = \dot{r}\hat{r}+r\dot{\theta}\hat{\theta}$$

Could you elaborate how you would approach this problem .Where should be the reference line of the angle measured ? How would we take into account that radius(the distance between the particle and the centroid) shrinks and gradually reduce to zero ?

 

[Saitama]

I haven't worked much with polar coordinates but I will give a try .

I know a couple of things .

$$ \vec{r} = r\hat{r}$$
$$ \vec{v} = \dot{r}\hat{r}+r\dot{\theta}\hat{\theta}$$

Could you elaborate how you would approach this problem .Where should be the reference line of the angle measured ? How would we take into account that radius(the distance between the particle and the centroid) shrinks and gradually reduce to zero ?

Yes, those equations work.

Now, use the fact that the speed of masses is constant. You need one more equation and you can obtain it from the ratio $\frac{r\dot{\theta}}{\dot{r}}$.

For the reference line, you can assume any initial positions you wish. :)

 

[Tanya Sharma]

Now, use the fact that the speed of masses is constant.

Do you mean $u = \sqrt{\dot{r}^2+(r\dot{\theta})^2)}$ ? How should I use it ?

You need one more equation and you can obtain it from the ratio $\frac{r\dot{\theta}}{\dot{r}}$.

What is $\frac{r\dot{\theta}}{\dot{r}}$ ? Is it the ratio of the tangential and radial component of velocity ?

 

[Saitama]

Do you mean $u = \sqrt{\dot{r}^2+(r\dot{\theta})^2)}$ ? How should I use it ?

The question states that the speed is constant. You have to use it with the relation you obtain between two components of velocity.

What is $\frac{r\dot{\theta}}{\dot{r}}$ ? Is it the ratio of the tangential and radial component of velocity ?

Yes. :)

 

[Tanya Sharma]

But what is the relation between the tangential and radial components of velocity ?

I do not understand what we are trying to achieve .Please elaborate the general idea .

 

[Saitama]

But what is the relation between the tangential and radial components of velocity ?

Do you see that the ratio is $\tan(5\pi/6)$?

I do not understand what we are trying to achieve .Please elaborate the general idea .

Well...a differential equation. :D

 

[Tanya Sharma]

Do you see that the ratio is $\tan(5\pi/6)$?

No . How did you get that ?

Well...a differential equation. :D

A differential equation in ?

 

[Saitama]

No . How did you get that ?

I am not sure about how should I explain it. I attached a figure, does it help?

Maybe, look at it this way:
$$\tan\frac{\pi}{6}=\frac{r\dot{\theta}}{-\dot{r}}$$

A differential equation in ?

The one you want. From two equations, you can find a differential equation in either $r$ and $t$ or $\theta$ and $t$.