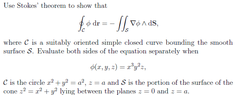Solving the Mystery of Crossproduct with Integral and Stokes' Theorem

[GreenGoblin]

View attachment 152

^ I had to copy in the question as an img because I don't know how to tex some of the symbols. Hope this is ok...

Basically my understanding of this question is that it doesn't make sense? How can you have crossproduct with an integral operator?
This result looks similar to the definition of Stokes' theorem but it is not quite exact so... does anyone know if this even make sense or what am I seeing wrong?

As for the 'second' part of the question, should I just do line integral and surface integral and then compare result to show equality?

The way I see it the whole thing doesn't make sense since you can't cross a scalar function...

what does crossproduct with dS even mean? Is that going to be (d/dx, d/dy, d/dz)? I can do that if so but I don't know that I would be doing the right thing. Either way I don't know how Stokes Theorem can be used to show this relationship because the function is a scalar not vector..

 

[HallsofIvy]

I think you are misreading "dS". Because it is in bold face type, like the "r" in "dr", it is a vector differential, not a scalar.

When S is a surface, dS is the "differential of surface area", a numerical valued function that, at each point, reflects the area of an infinitesmal section of the surface. dS, or d\vec{S}, however, is the "vector differential of surface area". It is a vector field, normal to the surface at each point, whose length is dS.

 

[GreenGoblin]

I do know that but I don't see how it corresponds with Stokes Theorem, it is not the same form at all..
So I don't know how to tackle this quesiton

Also the LHS, is supposed to be a vecotr function with the dr (I know the buld is vector, I have this notes) BUT we have the function (the o with the dash through, i don't know which you cal lthis letter is epsilon or theta or what?) however we have a scalar function, how you can apply this with VECTOR operator?

the RHS, i get it know we can make a fector from GRADient operator x the funciton and then crossproduct the dS

but my question is, how you can apply the LHS and also, what is the VECtor dS (is it partials? df/dx, df/dy, dfd/z?) or what?

how does the fact it is a cone come into play? the surface of a cone is just a circle disc.

 

[HallsofIvy]

The "generalized Stokes theorem" says the \int_{\partial S} \omega= \int_{S} d\omega. "Green's theorem", "Stoke's theorem", etc. are special cases.

No, the "surface of a cone" is NOT the circle disk at its base. In this case, where we are dealing with a surface and its boundary, the surface of the cone is the slant surface of the cone. The boundary is the circle.

 

[Opalg]

The first thing you have to do for this problem is to parametrise the curve $C$ and the surface $S$. The natural parametrisation is to write $\mathbf{r} = (a\cos\theta, a\sin\theta,a)$ for a point on $C$, and $\mathbf{S} = (t\cos\theta,t\sin\theta,t)$ for a point on $S$ (where $0\leqslant\theta\leqslant2\pi$ and $0\leqslant t\leqslant a$).

Then (differentiating with respect to $\theta$) $d\mathbf{r} = (-a\sin\theta, a\cos\theta,0)d\theta$. Thus $$\oint_Cx^3y^2z\,d\mathbf{r} = \int_0^{2\pi}a^3\cos^3\theta a^2\sin^2\theta a(-a\sin\theta, a\cos\theta,0)d\theta = a^7\int_0^{2\pi}(-\cos^3\theta\sin^3\theta, \cos^4\theta\sin^2\theta,0)\,d\theta.$$

For the surface integral, you first have to determine the normal vector $d\mathbf{S}$. To do that, write down the partial derivatives $\frac{\partial \mathbf{S}}{\partial t} = (\cos\theta,\sin\theta,1)$ and $\frac{\partial \mathbf{S}}{\partial \theta} = (-t\sin\theta,t\cos\theta,0)$. Their cross product is the normal vector to the surface, namely $d\mathbf{S} = (-t\cos\theta,-t\sin\theta,t)\,dt\, d\theta$.

Next, form the gradient $\nabla\phi = (3x^2y^2z,2x^3yz,x^3y^2) = t^5(\cos^2\theta\sin^2\theta,2\cos^3\theta\sin \theta,\cos^3\theta\sin^2\theta)$, and form its cross product with $d\mathbf{S}$ to get $$\iint_S\nabla\phi\wedge d\mathbf{S} = \int_0^{2\pi}\int_0^a t^6(2\cos^3\theta\sin\theta+\cos^3\theta \sin^3 \theta,-\cos^4\theta \sin^2\theta-3\cos^2\theta \sin^2\theta, -3\cos^2\theta \sin^3 \theta+2\cos^4\theta \sin\theta)\,dt\,d\theta.$$

Your job now is to evaluate those integrals, by integrating each coordinate in turn. It looks fairly horrendous, but you should note that an integral of the form$\displaystyle\int_0^{2\pi}\cos^m\theta\sin^n \theta\,d\theta$ is zero except when the integers $m$ and $n$ are both even.

 

[GreenGoblin]

hello
thank you opalg very much
i did not know dS is itself a crossproduct

i am fine with evaluating now

however...
the first part says "use stokes threm to show this... etc" now this is wherre the marks are i think.. and this what i need to do.
what i really don't get is that stokes theorem needs a fector function, but f is a scalar here

what is it asking?
do you need to take one side of stokes theorem, show it equals one side of this?or what?
'show' question are hard

ALSO Just as an aside:
do i really care that it is a "CONE" how it does affect the question at all? all u instructed me seems so simple as a process of calculations.. from what you write is is so easy to follow but i don't see its "cone" property as relevant anywhere? so why i care it a cone?

gracias