Solving the Mystery of the Table: Explaining $g = (123)$

In summary, the function $g$ takes theinput $123$ and returns the output $(123)(1)$, $(123)$ and $(123)(12)$.
  • #1
Guest2
193
0
View attachment 5399

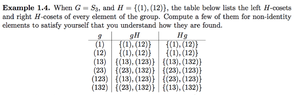
Could someone please explain how they're getting the answers in the table, for example $g = (123)$.
 

Attachments

  • Screen Shot 2016-03-14 at 13.53.08.png
    Screen Shot 2016-03-14 at 13.53.08.png
    23.3 KB · Views: 81
Physics news on Phys.org
  • #2
$$(123)(1)$$

$(123)$ represents the function that maps $1$ to $2$, $2$ to $3$ and $3$ to $1$.
$(1)$ represents the identity function, i.e. the function that maps $1$ to $1$, $2$ to $2$ and $3$ to $3$.

So to compute $(123)(1)$ we do the following:

From the right cycle we have that $1$ is mapped to $1$, and at the first cycle $1$ is mapped to $2$, therefore we get that $1$ is mapped to $2$.
From the right cycle we have that $2$ is mapped to $2$, and at the first cycle $2$ is mapped to $3$, therefore we get that $2$ is mapped to $3$.
From the right cycle we have that $3$ is mapped to $3$, and at the first cycle $3$ is mapped to $1$, therefore we get that $3$ is mapped to $1$.

So, we get $(123)(1)=(123)$.
$$(123)(12)$$

$(123)$ represents the function that maps $1$ to $2$, $2$ to $3$ and $3$ to $1$.
$(12)$ represents the function that maps $1$ to $2$, $2$ to $1$ and $3$ to $3$.

So to compute $(123)(12)$ we do the following:

From the right cycle we have that $1$ is mapped to $2$, and at the first cycle $2$ is mapped to $3$, therefore we get that $1$ is mapped to $3$.
From the right cycle we have that $2$ is mapped to $1$, and at the first cycle $1$ is mapped to $2$, therefore we get that $2$ is mapped to $2$.
From the right cycle we have that $3$ is mapped to $3$, and at the first cycle $3$ is mapped to $1$, therefore we get that $3$ is mapped to $1$.

So, we get $(123)(12)=(13)$.
 
  • #3
mathmari said:
$$(123)(1)$$

$(123)$ represents the function that maps $1$ to $2$, $2$ to $3$ and $3$ to $1$.
$(1)$ represents the identity function, i.e. the function that maps $1$ to $1$, $2$ to $2$ and $3$ to $3$.

So to compute $(123)(1)$ we do the following:

From the right cycle we have that $1$ is mapped to $1$, and at the first cycle $1$ is mapped to $2$, therefore we get that $1$ is mapped to $2$.
From the right cycle we have that $2$ is mapped to $2$, and at the first cycle $2$ is mapped to $3$, therefore we get that $2$ is mapped to $3$.
From the right cycle we have that $3$ is mapped to $3$, and at the first cycle $3$ is mapped to $1$, therefore we get that $3$ is mapped to $1$.

So, we get $(123)(1)=(123)$.
$$(123)(12)$$

$(123)$ represents the function that maps $1$ to $2$, $2$ to $3$ and $3$ to $1$.
$(12)$ represents the function that maps $1$ to $2$, $2$ to $1$ and $3$ to $3$.

So to compute $(123)(12)$ we do the following:

From the right cycle we have that $1$ is mapped to $2$, and at the first cycle $2$ is mapped to $3$, therefore we get that $1$ is mapped to $3$.
From the right cycle we have that $2$ is mapped to $1$, and at the first cycle $1$ is mapped to $2$, therefore we get that $2$ is mapped to $2$.
From the right cycle we have that $3$ is mapped to $3$, and at the first cycle $3$ is mapped to $1$, therefore we get that $3$ is mapped to $1$.

So, we get $(123)(12)=(13)$.
Wonderful explanations, thanks!
 
  • #4
mathmari said:
$$(123)(1)$$

$(123)$ represents the function that maps $1$ to $2$, $2$ to $3$ and $3$ to $1$.
$(1)$ represents the identity function, i.e. the function that maps $1$ to $1$, $2$ to $2$ and $3$ to $3$.

So to compute $(123)(1)$ we do the following:

From the right cycle we have that $1$ is mapped to $1$, and at the first cycle $1$ is mapped to $2$, therefore we get that $1$ is mapped to $2$.
From the right cycle we have that $2$ is mapped to $2$, and at the first cycle $2$ is mapped to $3$, therefore we get that $2$ is mapped to $3$.
From the right cycle we have that $3$ is mapped to $3$, and at the first cycle $3$ is mapped to $1$, therefore we get that $3$ is mapped to $1$.

So, we get $(123)(1)=(123)$.

$$(123)(12)$$

$(123)$ represents the function that maps $1$ to $2$, $2$ to $3$ and $3$ to $1$.
$(12)$ represents the function that maps $1$ to $2$, $2$ to $1$ and $3$ to $3$.

So to compute $(123)(12)$ we do the following:

From the right cycle we have that $1$ is mapped to $2$, and at the first cycle $2$ is mapped to $3$, therefore we get that $1$ is mapped to $3$.
From the right cycle we have that $2$ is mapped to $1$, and at the first cycle $1$ is mapped to $2$, therefore we get that $2$ is mapped to $2$.
From the right cycle we have that $3$ is mapped to $3$, and at the first cycle $3$ is mapped to $1$, therefore we get that $3$ is mapped to $1$.

So, we get $(123)(12)=(13)$.

Spoken like a pro.
 

FAQ: Solving the Mystery of the Table: Explaining $g = (123)$

What is the significance of $g = (123)$ in solving the mystery of the table?

The notation $g = (123)$ represents a specific permutation or rearrangement of the numbers 1, 2, and 3. In this case, it indicates that the numbers are being rearranged in ascending order. This notation is commonly used in mathematics and physics to represent different types of transformations.

How does $g = (123)$ relate to the mystery of the table?

The mystery of the table refers to a specific problem or puzzle that involves rearranging numbers or objects in a specific pattern. The notation $g = (123)$ may be used to represent a step in the solution to this mystery, or it may be the final solution itself.

Can $g = (123)$ be written in a different form?

Yes, the notation $g = (123)$ is just one way to represent this particular permutation. Other common notations for permutations include cycle notation, where the numbers are written in a circular pattern, and matrix notation, where the permutation is represented as a matrix of 0s and 1s.

How is $g = (123)$ used in practical applications?

The notation $g = (123)$ can be used in a variety of scientific and mathematical fields to represent transformations or changes in a system. For example, it may be used in computer graphics to represent a specific rotation or reflection of an object, or in chemistry to represent the arrangement of atoms in a molecule.

Are there other permutations that could solve the mystery of the table?

Yes, there are many other permutations that could potentially solve the mystery of the table. $g = (123)$ is just one example, and it may not be the most efficient or elegant solution. Depending on the specific problem, there may be multiple valid solutions using different permutations.

Similar threads

MHB Finding a Cayley Table for a Groupoid: an Example
Replies
3
Views
2K
I Decomposing arbitrary representations
Replies
2
Views
1K
Insights How Quantum Information Theory Solves “the only mystery” of Quantum Mechanics
Replies
1
Views
4K
How to solve a circuit mystery box
Replies
8
Views
2K
Downdraft table -blocking off part of table surface to increase flow?
Replies
10
Views
2K
Why body A has greater acceleration?
Replies
13
Views
779
MHB Example on Triangular Rings - Lam, Example 1.14
Replies
4
Views
1K
MHB How Do You Manage Database Tables in SQL?
Replies
8
Views
841
A About Schur's lemma in lie algebra
Replies
2
Views
2K
MHB Dual Spaces .... Friedberg et al, Example 4, Section 2.6
Replies
2
Views
1K

Hot Threads

Recent Insights

Back
Top