ayahouyee
- 12
- 0
Im stuck on this question! so can someone please please help me? Thank you!
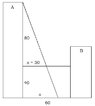
A tightrope is 40 ft above ground between two buildings that are 60 feet apart. A
tightrope walker starts along the rope and walks from building A to building B at
a rate of 2 feet per second. 80 feet above the starting point of the tightrope walker
on building A is a spotlight that is illuminating the tightrope walker as the tightrope
walker is crossing between the two buildings.
(a) How fast is the shadow of the tightrope walker's feet moving along the ground
when the tightrope walker is midway between the buildings?
(b) How fast is the shadow of the tightrope walker's feet moving up the wall of building
B when the tightrope walker is twelve feet away from building B?
A tightrope is 40 ft above ground between two buildings that are 60 feet apart. A
tightrope walker starts along the rope and walks from building A to building B at
a rate of 2 feet per second. 80 feet above the starting point of the tightrope walker
on building A is a spotlight that is illuminating the tightrope walker as the tightrope
walker is crossing between the two buildings.
(a) How fast is the shadow of the tightrope walker's feet moving along the ground
when the tightrope walker is midway between the buildings?
(b) How fast is the shadow of the tightrope walker's feet moving up the wall of building
B when the tightrope walker is twelve feet away from building B?