alan123hk
- 817
- 450
I saw a book that uses special relativity to solve the twin paradox, the inference process is roughly as follows.
Suppose a spacecraft sets off from the Earth to travel to a distance black hole and then return to the earth. We divide this process into three stages, that is, the process of navigating to this black hole (a→ b), the short moment of reverse turning (b→c) and the process of homing (c→d).
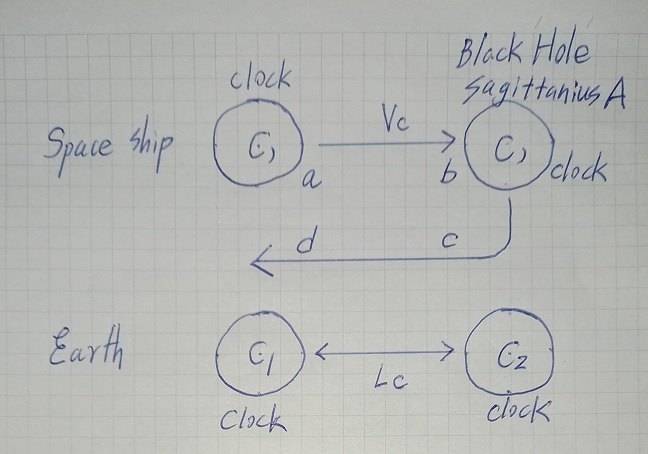
Vc = speed of the spacecraft , in light year
Lc = distance between the Earth and the black hole, in light year
The following is from the perspective of an observer in the spacecraft .
When he reached the black hole (a→ b), he found that the time of C2 was ##\left( \frac {L_c} {V_c} \right) ##, but he doesn't think this is the time elapsed by the observer on earth, because he thinks that the time of C2 is already ## \left( \frac {V_c L_c} {c^2} \right) ## faster than the C1, so the actual elapsed time of the Earth should be ## \left( \frac {L_c} {V_c} -\frac {V_c L_c}{c^2} \right)##
The moment the spacecraft turns to go in opposite direction (b→c) , he found that time of C1 suddenly changed from ## \left( \frac {V_c L_c} {c^2} \right) ## behind C2 to ## \left( \frac {V_c L_c} {c^2} \right) ## ahead of C2, so the time on Earth suddenly increased by ## \left( 2\frac {V_c L_c} {c^2} \right) ##
When the spacecraft returns (c→d), the Earth also passed time ## \left( \frac {L_c} {V_c} -\frac {V_c L_c}{c^2} \right)##
So in the end, the observer in the spacecraft thinks that the total elapsed time of the observer on the Earth is ##\left[ 2 \left( \frac {L_c} {V_c} -\frac {V_c L_c}{c^2}\right) + 2\frac {L_c V_c} {c^2} = 2\frac {L_c} {V_c} \right] ##, which is elapsed time by the observer on the earth.
On the other hand, the time elapsed by the observer in the spacecraft can be calculated from the observer on the Earth according to the time dilation, which is ##\left[\left( 2\frac {L_c}{V_c} \right) \sqrt {1-\frac {V_c^2} {C^2}} \right] ##
The final conclusion is that the ratio of time elapsed on Earth to the time elapsed in the spacecraft is ## \frac {1} { \sqrt {1-\frac {V_c^2} {C^2}}} ## , so for this twin brother, the brother who came back from the spacecraft is younger than the brother on earth.
I admire the above derivation process described in this book, but I still have a question in my heart, because the uniform linear motion is relative, why the observer on the Earth can’t think that the spacecraft is not in motion, but it is actually he carries the clock C1 Move in the opposite direction with the earth? So in this case, will observers on Earth come to the completely opposite conclusion?
Suppose a spacecraft sets off from the Earth to travel to a distance black hole and then return to the earth. We divide this process into three stages, that is, the process of navigating to this black hole (a→ b), the short moment of reverse turning (b→c) and the process of homing (c→d).
Vc = speed of the spacecraft , in light year
Lc = distance between the Earth and the black hole, in light year
The following is from the perspective of an observer in the spacecraft .
When he reached the black hole (a→ b), he found that the time of C2 was ##\left( \frac {L_c} {V_c} \right) ##, but he doesn't think this is the time elapsed by the observer on earth, because he thinks that the time of C2 is already ## \left( \frac {V_c L_c} {c^2} \right) ## faster than the C1, so the actual elapsed time of the Earth should be ## \left( \frac {L_c} {V_c} -\frac {V_c L_c}{c^2} \right)##
The moment the spacecraft turns to go in opposite direction (b→c) , he found that time of C1 suddenly changed from ## \left( \frac {V_c L_c} {c^2} \right) ## behind C2 to ## \left( \frac {V_c L_c} {c^2} \right) ## ahead of C2, so the time on Earth suddenly increased by ## \left( 2\frac {V_c L_c} {c^2} \right) ##
When the spacecraft returns (c→d), the Earth also passed time ## \left( \frac {L_c} {V_c} -\frac {V_c L_c}{c^2} \right)##
So in the end, the observer in the spacecraft thinks that the total elapsed time of the observer on the Earth is ##\left[ 2 \left( \frac {L_c} {V_c} -\frac {V_c L_c}{c^2}\right) + 2\frac {L_c V_c} {c^2} = 2\frac {L_c} {V_c} \right] ##, which is elapsed time by the observer on the earth.
On the other hand, the time elapsed by the observer in the spacecraft can be calculated from the observer on the Earth according to the time dilation, which is ##\left[\left( 2\frac {L_c}{V_c} \right) \sqrt {1-\frac {V_c^2} {C^2}} \right] ##
The final conclusion is that the ratio of time elapsed on Earth to the time elapsed in the spacecraft is ## \frac {1} { \sqrt {1-\frac {V_c^2} {C^2}}} ## , so for this twin brother, the brother who came back from the spacecraft is younger than the brother on earth.
I admire the above derivation process described in this book, but I still have a question in my heart, because the uniform linear motion is relative, why the observer on the Earth can’t think that the spacecraft is not in motion, but it is actually he carries the clock C1 Move in the opposite direction with the earth? So in this case, will observers on Earth come to the completely opposite conclusion?
Last edited: