Solving Thevenin's Equation for 2V Source Power

[maxsthekat]

Homework Statement
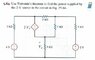
I have to find the power delivered by the 2v source (see "Thevenin1.jpg" -- attached)

The attempt at a solution
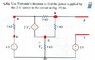
(See "Thevenin2.jpg") I started by placing my equivalent nodes at X and Y. Since this circuit has both dependent and independent sources, I used nodal analysis to attempt to find the voltage across these terminals (Voc).

My nodal equations were:

Node AC) (Va - Vd)/1k + Vc/1k + (Va-Vb)/2k = (Vb - Vc)/1k
Node B) (Va - Vb)/2k = (Vb - Vc)/2k
Vd = 4
2Vx = Va - Vc
Vx = Vc

Solving this, I got the following voltages {Va, Vb, Vc, Vd} = {3, 5/3, 1, 4}. This means the equivalent voltage (Voc) is 5/3 - 2 = -1/3 volts

Next, I tried to "short" the connection between X->Y to find the equivalent current (see "Thevenin3.jpg").

Again, applying nodal analysis:

Node AC) (Va - Vd)/1k + Vc/1k + (Va -Vb)/2k = (Vb - Vc)/1k
Vb = 2
Vd = 4
2Vx = Va - Vc
Vx = Vc

Which gave the following voltages {A, B, C, D} = {~3.6923, 2, ~1.2308, 4}

Plugging these back into the circuit to get the currents I_1, and I_2, I got:
I_1 = 4mA
I_2 = ~1.23mA
Thus, the I_sc current through the 2v source is ~2.77ma

Which means the equivalent resistance is (1/3 volts) / (~2.77 mA) = ~120.336 Ohm

Now, using the equivalent voltage and resistance, I plugged the 1k resistor back in, combined the two (since they're in series) for a total resistance of 1120.336 Ohm, and used this to find the current: (1/3)/(1120.336) ~ 0.30mA, which I then used to compute the power from the voltage source: 2 (volts) * 0.30 mA = .6 mW.

However, this is wrong... According to the answer key, it should be 0.32mW.

Can anybody help spot where I'm going wrong?

Thanks!

-Max

 

[maxsthekat]

Erm... Can someone approve the attachments, please?

 

[The Electrician]

I would think that the mesh method would be easier to use since you won't have to deal with any "supernodes".

There are 3 obvious meshes. From left to right, label the mesh currents I1, I2 and I3. Assuming the current in each mesh is counterclockwise, and setting the 2 volt source to zero, you will have:

2000*I1 + 0*I2 - 1000*I3 = 4 - 2*(1000*I1 - 1000*I3)

0*I1 + 3000*I2 - 1000*I3 = 2*(1000*I1 - 1000*I3)

-1000*I1 - 1000*I2 + 3000*I3 = 0

Solving, you should get:

I1 = 1/625 = 1.6mA
I2 = 1/1250 = .8 mA
I3 = 1/1250 = .8 mA

Isc, the Thevenin short circuit current, is equal to I3.

To get Vth, solve a reduced system, one with the 2 volt source absent. Then there are only 2 mesh currents:

2000*I1 + 0*I2 = 4 - 2*(1000*I1)

0*I1 + 3000*I2 = 2*(1000*I1)

Solving:

I1 = 1/1000
I2 = 1/1500

The open circuit Thevenin voltage is just the sum of the voltage drops across the two middle 1k resistors.

Vth = 1000*I1 + 1000*I2 = 5/3 volts

Then, Rth is (5/3)/.8 mA = 2083.33 ohms.

From here, the rest is easy.

 

[WmasterX]

Can Someone Resolve my Execrise .. please .

 

[hadiffina]

Can Someone Resolve my Execrise .. please .

using nodal analysis and place a test voltage, V on the node which is on the 2Amp source
current into node = current out of node
2A = (V-12)/6 + V/10 and solve for V

once you had determined value of V , use voltage divider to obtain voltage drop on the 4ohm resistor (which is Vab)

Vab = (4/10) X V;
Vth = Vab

To find Rth, short out 12V voltage source and open the 2A current source and you will see
that (6ohm + 6ohm) parallel to 4ohm solve it and youll get the answer

plug in Vth and Rth to the load to get value of i

 

[vela]

These two combinations are equivalent: a voltage source V in series with a resistor R, and a current source I in parallel with a resistor R, where V=IR.

So to start, you can replace the 12-V voltage source in series with the 6-ohm resistor by a 2-A current source in parallel with a 6-ohm resistor. Parallel current sources add, so you can combine the two in the circuit into one. Then you'll find it's in parallel with a resistor, so you can replace that combination with its Thevenin equivalent. And so on.

Just keep transforming the circuit one step at a time, and you'll eventually get to the solution.

 

[WmasterX]

i know to resolve resistor .. but the source of 2A confuse me ... :S i know to resolve with two source witch is with Voltage , but in this case i have source 2A witch getting me confused ...

 

[vela]

So you're having trouble finding the open-circuit voltage across A-B? What have you tried so far?

 

[utkarsh1]

My suggestion for this kind of circuit is using source transformation to simplify the circuit and then use thevenin theorem, makes life much easier and it is very very fast.
Do the following for source transformation:

i) you can take 12V source and 6K resistor in series with source and transform it to 2 A source in upward direction with 6K resistor in parallel

ii) Now you can combine 2 * 2A sources into 4A sources with 6K in parallel.

iii) convert sources back to voltage source: 4A * 6K = 24V with 6K in series

iv) now combine 2 * 6K series resistors to 12K resistors.

V) Now Do open voltage at node: and you can simply see it is 4/16 * 24 = 6V
Vi) and equivalent resistor: 12 // 4 = 3K
vII) and you have your network

This took me all of about 2 mins. without calculator too. SO My advice for DC circuits exploit the SOURCE Transformation it is extremely useful concept

Can Someone Resolve my Execrise .. please .

 

[WmasterX]

A lot of thanks to everyone for the help :)