Solving Two Layer Fluid Flow with Different Viscosities and Equal Densities

[thshen34]

Following this example,

http://www.creatis.insa-lyon.fr/~dsarrut/bib/others/phys/www.jwave.vt.edu/crcd/batra/lectures/esmmse5984/node53.html

I know you can solve for v by integrating the equations along with boundary conditions.

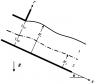
How would you solve a problem where you have another layer on top of the original fluid? Such as in the attached picture.

You can assume the densities are equal, but the viscosities are different

 

[K41]

Wouldn't you just have two equations and two unknowns?

 

[Chestermiller]

If the flow is steady, first do a shell force balance to determine how the shear stress is varying with distance measured normal to the upper surface. The shear stress at the upper surface is zero. Once you know how the shear stress is varying, you can use Newton's law of viscosity to get the velocity gradient versus position. Make sure you take into account the condition that the velocity gradient is discontinuous at the interface (because of the discontinuity in viscosity). You can then integrate to get the velocity as a function of position, taking into account that the velocity at the lower boundary is zero, and the velocity at the interface between the fluids is continuous.

 

[thshen34]

Hi,

Thanks for your input, but isn't this supposed to be done using the Navier Stokes equations?

That is how it was done for one layer. Could you provide some equations with what you are saying?

Thanks

 

[Chestermiller]

Hi,

Thanks for your input, but isn't this supposed to be done using the Navier Stokes equations?

That is how it was done for one layer. Could you provide some equations with what you are saying?

Thanks

Yes. Express the NS equations in coordinates perpendicular and parallel to the incline. You only need to use the equation parallel to the incline. Velocity is not changing along the direction parallel to the incline, and neither is the pressure. You are left with the ρgsinθ term and the second derivative of the velocity with respect to y term in the equation. You need to integrate twice with respect to y, and you need to match the shear stresses at the interface between the two fluids: η(dv/dy) is continuous at the interface, so dv/dy is discontinuous. You have zero shear stress (velocity gradient) at the top boundary, and zero velocity at the bottom boundary. This should give you your constants of integration.