Solving Two Worlds Spinning: Calculating Tension (T) in String

[soupastupid]

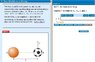
Homework Statement

There are two balls with masses m_a and m_b connected by a string. m_b is moving at a velocity v upwards (perpendicular to the string) and it asks for the Tension (T) in the string.

Homework Equations

a=(v^2)/R
delta Energy of system = 0

T = m((u^2)/r)
u is linear speed of rotational motion
r = radius of motion

The Attempt at a Solution

The initial kinetic energy of m_b = .5(m_b)v^2

and that's as far as I got.
Is mass B moving?

how do I start this problem?

 

[Doc Al]

Homework Equations

a=(v^2)/R

That will come in handy.

The initial kinetic energy of m_b = .5(m_b)v^2

Why did you calculate the energy?

and that's as far as I got.
Is mass B moving?

Mass B's velocity is described in the problem statement.

Hint: Viewed from the inertial lab frame, mass B is in pure rotation about mass A (at the instant shown). Apply Newton's 2nd law.