- #1
Solving Word Problem - Picture Guide
- Thread starter Miike012
- Start date
-
- Tags
- Word problem
In summary, you added a picture and your work is inside the picture. You need y(initial). So leave it on the right hand side of the equation and move everything else to the other side.
- #2
ehild
Homework Helper
- 15,542
- 1,917
You need y(initial). So leave it on the right hand side of the equation and move everything else to the other side.
ehild
ehild
- #3
Miike012
- 1,009
- 0
Wont that give me the same result?
- #4
ehild
Homework Helper
- 15,542
- 1,917
You will not be confused with the lot of minuses. Try to type in, I can not read your file.
ehild
ehild
- #5
Miike012
- 1,009
- 0
-(5)(2) - (9.8/2)(4) = y(init)... same thing
- #6
Miike012
- 1,009
- 0
actually I get 29.6... but its neg...
- #7
Miike012
- 1,009
- 0
shouldnt it be negative instead of pos?
- #8
vela
Staff Emeritus
Science Advisor
Homework Helper
Education Advisor
- 16,090
- 2,731
By using a=-g, you chose the upward direction to be positive. The ball is thrown downward, so what should the sign of vinit be?
- #9
ehild
Homework Helper
- 15,542
- 1,917
Miike012 said:
Your original equation is y=y(init)+v(init)t-(1/2) g t2
At the final position, y=0. g=9.8 m/s2, v(init)=-5 m/s,
So the equation is
y(init)-5*2 -(9.81/2)(4)=0 or y(init)-[5*2 +(9.81/2)(4)]=0
You subtract (10+9.81*2) from y(init) and you get zero. What is y (init)?
When solving an equation, we isolate the unknown at one side, by adding everything else to both sides or subtracting everything else form both sides, or multiplying/dividing both sides...
Add 5*2+(9.81/2)(4) to both sides now
ehild
- #10
Miike012
- 1,009
- 0
When working with free falling objects... In general... Is acceleration always calculated to be -9.80 in the equation?
because I origninally thought a = -g meaning -(1/2) (-g) t^2 = (1/2) (g) t^2
... but I see that the original equation already has a neg sign there for acc... "-" (1/2) g t^2.
because I origninally thought a = -g meaning -(1/2) (-g) t^2 = (1/2) (g) t^2
... but I see that the original equation already has a neg sign there for acc... "-" (1/2) g t^2.
- #11
ehild
Homework Helper
- 15,542
- 1,917
You can choose positive and negative direction arbitrary, but once decided, you must use it consequently.
g is posite, it means the magnitude of gravitational acceleration on the surface of the Earth. It is about 9.8 m/s2.
If you choose that y is height then the upward direction is positive. Gravity acts downward, so the acceleration is -g or -9.8 m/s2.
If you choose the quantity y as the displacement in downward direction, then the downward acceleration is positive and it is g=9.8 m/s2.
ehild
g is posite, it means the magnitude of gravitational acceleration on the surface of the Earth. It is about 9.8 m/s2.
If you choose that y is height then the upward direction is positive. Gravity acts downward, so the acceleration is -g or -9.8 m/s2.
If you choose the quantity y as the displacement in downward direction, then the downward acceleration is positive and it is g=9.8 m/s2.
ehild
- #12
Miike012
- 1,009
- 0
thankyou
- #13
Miike012
- 1,009
- 0
Sorry.. Let me see if I understand...
If distance is counted + in upward direction, then a = -g if an object is thrown upward...
If distance is counted + in upward direction, then a = g if an object is dropped from a building downward?
is this correct?
If distance is counted + in upward direction, then a = -g if an object is thrown upward...
If distance is counted + in upward direction, then a = g if an object is dropped from a building downward?
is this correct?
- #14
HallsofIvy
Science Advisor
Homework Helper
- 42,988
- 981
No, the acceleration due to gravity is always downward so if you take + in the upward direction, g is negative. It is the initial velocity that is positive if the object is thrown upward, negative if it is thrown downward, 0 if it is "dropped".
- #15
Miike012
- 1,009
- 0
Ok last question... I made downward direction neg... but in your about post you said
g=9.8 m/s2, why did u not say -9.8 m/s^2?
g=9.8 m/s2, why did u not say -9.8 m/s^2?
- #16
Miike012
- 1,009
- 0
Is it because the - sign is already in the equation?
- #17
vela
Staff Emeritus
Science Advisor
Homework Helper
Education Advisor
- 16,090
- 2,731
Yes, the equation is written assuming the upward direction is positive.
The original equation you learn for constant acceleration a is[tex]y=y_0+{v_y}_0 t+\frac{1}{2}at^2[/tex]If you take the upward direction to be positive, you have a=-g=-9.8 m/s2, so you get[tex]y=y_0+{v_y}_0 t-\frac{1}{2}gt^2[/tex]This is the equation you're using, so by using it, you've assumed the upward direction is positive. On the other hand, if you take the downward direction to be positive, you would have a=+g=+9.8 m/s2, so you get[tex]y=y_0+{v_y}_0 t+\frac{1}{2}gt^2[/tex]In both cases, g=+9.8 m/s2 since g is the magnitude of the acceleration due to gravity.
As ehild said, both ways will work, but you have to be consistent and adjust the signs on the various quantities depending on which convention you're following.
The original equation you learn for constant acceleration a is[tex]y=y_0+{v_y}_0 t+\frac{1}{2}at^2[/tex]If you take the upward direction to be positive, you have a=-g=-9.8 m/s2, so you get[tex]y=y_0+{v_y}_0 t-\frac{1}{2}gt^2[/tex]This is the equation you're using, so by using it, you've assumed the upward direction is positive. On the other hand, if you take the downward direction to be positive, you would have a=+g=+9.8 m/s2, so you get[tex]y=y_0+{v_y}_0 t+\frac{1}{2}gt^2[/tex]In both cases, g=+9.8 m/s2 since g is the magnitude of the acceleration due to gravity.
As ehild said, both ways will work, but you have to be consistent and adjust the signs on the various quantities depending on which convention you're following.
- #18
ehild
Homework Helper
- 15,542
- 1,917
Mike,
Suppose a body moves with uniform acceleration. Its position in terms of time is y(t)=y(init) + v(init) t+a/2 t2.
In case gravity is the only force acting on the body, you know that it accelerates downward, and the magnitude of the acceleration is g=9.8 m/s2. The value of g can be given with more or less accuracy, and it is different at different places of Earth, but it is always a positive number.
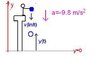
Before you start to solve a problem you draw a figure and show what direction you mean positive. You should choose the sign of both the acceleration and initial velocity with respect to this direction.
In the problem, y(init) is positive, and the position of the stone is always positive till it reaches the ground, where y is defined zero.
The initial velocity is downward, so it is negative, -5 m/s. Have been the stone thrown upward, the initial velocity would be positive.
The acceleration is downward, and its magnitude is equal to g, so a=-g =-9.8 m/s2. So your equation is
y(t)=y(init)-5t-9.8/2 t2.
ehild
Suppose a body moves with uniform acceleration. Its position in terms of time is y(t)=y(init) + v(init) t+a/2 t2.
In case gravity is the only force acting on the body, you know that it accelerates downward, and the magnitude of the acceleration is g=9.8 m/s2. The value of g can be given with more or less accuracy, and it is different at different places of Earth, but it is always a positive number.
Before you start to solve a problem you draw a figure and show what direction you mean positive. You should choose the sign of both the acceleration and initial velocity with respect to this direction.
In the problem, y(init) is positive, and the position of the stone is always positive till it reaches the ground, where y is defined zero.
The initial velocity is downward, so it is negative, -5 m/s. Have been the stone thrown upward, the initial velocity would be positive.
The acceleration is downward, and its magnitude is equal to g, so a=-g =-9.8 m/s2. So your equation is
y(t)=y(init)-5t-9.8/2 t2.
ehild
Attachments
FAQ: Solving Word Problem - Picture Guide
What is the purpose of using a picture guide to solve word problems?
The purpose of using a picture guide to solve word problems is to visually represent the information given in the problem. This can help individuals better understand the problem and identify the necessary steps to solve it.
What are some common steps to follow when using a picture guide to solve word problems?
Some common steps to follow when using a picture guide to solve word problems are: 1) carefully reading and understanding the problem, 2) identifying the relevant information and variables, 3) drawing a picture or diagram to represent the problem, 4) labeling the picture with the given information and unknowns, and 5) using the picture to set up and solve the problem.
How can a picture guide help in solving complex word problems?
A picture guide can help in solving complex word problems by breaking down the problem into smaller, more manageable parts. By visually representing the problem, individuals can better understand the relationships between different pieces of information and how they contribute to the overall solution.
What are the benefits of using a picture guide to solve word problems?
Using a picture guide to solve word problems can have several benefits, including: 1) promoting visual learning, 2) improving problem-solving skills, 3) enhancing critical thinking skills, 4) increasing comprehension of the problem, and 5) providing a clear and organized approach to problem solving.
Are there any limitations to using a picture guide to solve word problems?
While using a picture guide can be helpful, it may not be suitable for all types of word problems. Some problems may not lend themselves well to visual representation, and individuals may have different learning styles that may require a different approach. Additionally, the use of a picture guide may not be feasible in certain situations, such as timed tests or exams.