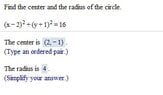Solving (x-h)^2+(y-k)^2=r^2: Reverse + to - & Square?

[OMGMathPLS]

View attachment 3289

So... you just reverse the - and positive sign and square the ending =? Is that how you solve this?

Because writing it out does not make sense. How do you go from positive to turning it into a negative?

 

[MarkFL]

Yes, a circle of the form:

$$(x-h)^2+(y-k)^2=r^2$$

Is centered at $(h,k)$ and has radius $r$. Your given circle may be written as:

$$(x-2)^2+(y-(-1))^2=4^2$$

And so its center is $(2,-1)$ and its radius is $4$.

 

[OMGMathPLS]

The h,k are the relation, the origin co-ordinates, right? The center of the circle?

And this is part of the Pythagorean theorem but we are just adding in the x and y coordinates to shift it, right?

 

[MarkFL]

The h,k are the relation, the origin co-ordinates, right? The center of the circle?

And this is part of the Pythagorean theorem but we are just adding in the x and y coordinates to shift it, right?

The way I look at it, a circle is defined to be the locus of all points a given distance, the radius $r$, from some central point, the focus or center. If we let the center be at $(h,k)$, and an arbitrary point on the circle be $(x,y)$, then the distance formula gives us:

$$\sqrt{(x-h)^2+(y-k)^2}=r$$

And then squaring, we obtain:

$$(x-h)^2+(y-k)^2=r^2$$

 

[OMGMathPLS]

So if it's actually a positive we always have to keep it as a negative by turning it into a -(-) .

Do you know what its an h and k? This is really confusing me. In other countries it's called an a and b right? I found when I think of hong kong the hong is the x and the kong is the y it helps but it just makes no sense why it's h,k especially if that was arbitrary.

Thanks for your answer.

 

[MarkFL]

Yes, the use of $h$ and $k$ in this context are just an arbitrary convention used here in the U.S., and perhaps in other places as well. You can use any parameters for the center that you want, such as $(a,b)$.