- #1
Wasif Jalal
- 1
- 0
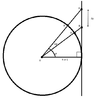
Show that y≈∆φ×secφ in the jpeg attached.
or ∆y = sec φ
A and B are points on curved surface, two lines are extended through origin to a line that is tangent to the circle, these points are A' and B', change in Angle will bring a change in length between A' and B'. I need to know how is this do-able.View attachment 7296[ATTACH=
or ∆y = sec φ
A and B are points on curved surface, two lines are extended through origin to a line that is tangent to the circle, these points are A' and B', change in Angle will bring a change in length between A' and B'. I need to know how is this do-able.View attachment 7296[ATTACH=
Attachments
Last edited: