Some questions about baryogenesis

[Barry-O-Genesis]

TL;DR Summary

I have some basic questions about how protons and anti-protons are formed.

I'm trying to follow Scott Dodelson's Modern Cosmology. Specifically Chapter 3. Coverage of the subject of baryogenesis appears to be missing from Dodleson's book, so I'm trying to reconstruct things on my own.

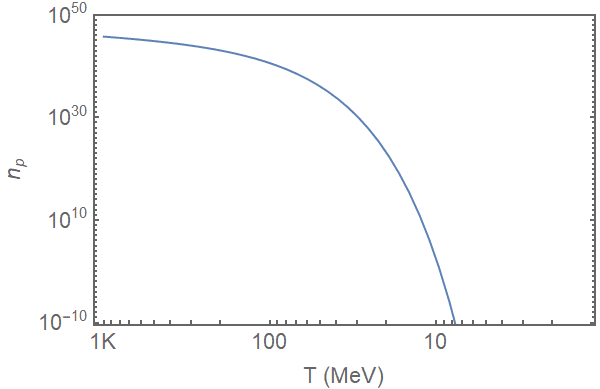
This represents the formula:$$n_p[T]=g_p\space (\frac{k_b\space m_p\space T}{2\pi \hbar})^{\frac{3}{2}}\space e^{-\frac{c^2m_p}{k_B\space T}}$$which should be the same as formula (3.6) in SI units. So, my questions are:

1. I'm a little confused about what this number is, exactly. Does this represent the number of protons in a unit volume as long as the protons are in equilibrium with their surroundings? If we're working in SI units, is this the number of protons that I'd find in a cubic meter as a function of temperature (time)?

2. Isn't there supposed to be some event that causes proton creation to eventually stop and for the change in proton density to be governed only by the expansion of space from that point out ("freeze-out")? Don't we need the reaction rate ($\gamma+\gamma=p+\bar p$) and the expansion rate ($H$) to know when "freeze-out" occurs? Where can I find a lucid discussion of this?

3. As I interpret this chart, the number of baryons today should be effectively zero. If the plasma stayed in equilibrium down to the 7 MeV range, then certainly the protons would have been converted into other particles (photons). Yes, I understand the same can be said of antimatter, but it seems like you don't even need anti-protons to make the argument that - according to this formula - there should be no protons (baryons) a $0 MeV$. Am I reading this chart incorrectly?

 

[kimbyd]

Baryogenesis generally refers not to the "freeze-out" of baryons, but instead to the CP-breaking physics which created the imbalance between normal matter and anti-matter. This is currently an unsolved problem in theoretical physics. This field of study is usually more aligned with high-energy physics than cosmology.

The freeze-out of baryons is part of Big Bang Nucleosynthesis, which Dodelson starts talking about in 3.2. For the purposes of cosmology, it's generally just assumed that there are some number of protons at low temperatures, and at high temperatures there are those protons plus thermal proton/anti-proton pairs (edit: not protons, baryons. Mix of neutrons and protons at low energies). It is those thermal proton/anti-proton pairs that that equation describes, I believe.

As for the dependence upon the expansion, since the thermal proton/anti-proton particles are thermal, their number density is fully-defined by the temperature.