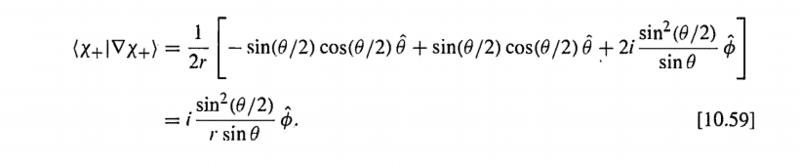Some questions in "Introduction to quantum mechanics"

[heslaheim]

TL;DR Summary

How to calculate the integral of a loop when the surface integrals of its curl are different in the area of different surface?

A certain field has a singularity at the origin, and the divergence of its curl is zero at any point outside the origin, but surface integral of the curl is not zero in the area of any closed surface containing the origin. So how should the Stokes theorem related to this field be expressed at this time?

 

[andresB]

I'm not sure to understand your question, but note that the Berry connection has zero component in the r direction. Hence for the surface you can be take the surface of a sphere of radius 1 (or whatever) and for the stokes theorem the path of the line integral can be taken to be lying also on the surface of the sphere.

Your question is strange to me since the Berry phase is usually presented first as a line integral of the Berry connection and then the Stokes theorem is invoked to express the holonomy as surface integral of the Berry curvature. So, first you have the loop in parameter space and then you can assign any surface with that loop as boundary to use in the surface integral.