Some works can be done simultaneously

  • MHB
  • Thread starter evinda
  • Start date
  • Tags
    Works
In summary: Yes... we're building up to that...We can create a timeline and keep track of the earliest time that each part can be completed. (Thinking)
  • #1
evinda
Gold Member
MHB
3,836
0
Hello! (Wave)

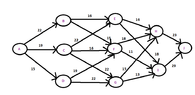
The nodes $A,B,C,D,E,F,G,H,I$ are given and are related as follows:View attachment 5084

The nodes $B,C,D,E,F,G,H,I$ are tasks that are done so that a work is completed , for example a building, and the cost $p(a,b)$ are the days that are needed so that the work $b$ finishes if the work $a$ has already finished.
For example, $p(A,B)=22$: 22 days are needed so that the work B is done.
$p(B,E)$: 16 days are needed so that the work E is done if the work B has finished.

Of course, some works can be done simultaneously.

Find the minimum time needed so that the building gets finished.How do we use the fact that some works can be done simultaneously?
 

Attachments

  • grw.png
    grw.png
    8 KB · Views: 80
Physics news on Phys.org
  • #2
Hey evinda! (Smile)

Suppose we would only need $A,B,C$.
How much time would that take? (Wondering)
 
  • #3
I like Serena said:
Hey evinda! (Smile)

Suppose we would only need $A,B,C$.
How much time would that take? (Wondering)

22 days? (Thinking)
 
  • #4
evinda said:
22 days? (Thinking)

Exactly!
So how long will it take to complete $D, E$ additionally? (Wondering)
 
  • #5
I like Serena said:
Exactly!
So how long will it take to complete $D, E$ additionally? (Wondering)

So in this case do we have to complete all the works $B, C, \dots, I$ so that the whole work is completed?

If so, then don't we make $B, C, D$ simultaneously and if we have completed for example $D$ we start with one of $G$ or $F$ ? (Thinking)
 
  • #6
evinda said:
So in this case do we have to complete all the works $B, C, \dots, I$ so that the whole work is completed?

If so, then don't we make $B, C, D$ simultaneously and if we have completed for example $D$ we start with one of $G$ or $F$ ? (Thinking)

How so?
Can't we complete just $B,C,D,E$? (Wondering)

And yes, we should indeed complete $B, C, D$ simultaneously.
 
  • #7
I like Serena said:
How so?
Can't we complete just $B,C,D,E$? (Wondering)

Don't we have to reach at $J$ , which is the last work?
 
  • #8
evinda said:
Don't we have to reach at $J$ , which is the last work?

Yes... we're building up to that...
We can create a timeline and keep track of the earliest time that each part can be completed. (Thinking)
 

FAQ: Some works can be done simultaneously

What does it mean for some works to be done simultaneously?

Simultaneous work refers to the ability to complete multiple tasks at the same time, rather than sequentially. This can save time and increase efficiency in certain situations.

Is it always possible for works to be done simultaneously?

No, it is not always possible for works to be done simultaneously. It depends on the nature of the tasks and the resources available. Some tasks may require full attention and cannot be done simultaneously with other tasks.

What are the benefits of completing works simultaneously?

The main benefit of completing works simultaneously is that it can save time and increase productivity. It also allows for better time management and the ability to handle multiple tasks at once.

Are there any disadvantages to doing works simultaneously?

One disadvantage of doing works simultaneously is that it can lead to a lack of focus and quality in the work being done. It also requires good multitasking skills and can be overwhelming for some individuals.

How can one determine which tasks can be done simultaneously?

The best way to determine which tasks can be done simultaneously is to analyze the nature of the tasks and the resources available. Tasks that require similar resources and do not require full attention can usually be done simultaneously.

Similar threads

I Finding CDF given boundary conditions (simple stats and calc)
Replies
10
Views
2K
MHB Please help with bool algebra and logic things
Replies
2
Views
1K
Chernoff Bounds using importance sampling identity
Replies
0
Views
1K
B Work Done By Conservative Forces
Replies
1
Views
752
A Computing a variance in astrophysics context
Replies
1
Views
1K
I Sign convention on work done to a closed system containing gas
Replies
5
Views
2K
I Intro to Symbolic Logic: Replacement Rules
Replies
8
Views
2K
How should I show that the transformation makes the system Hamiltonian?
Replies
4
Views
612
B What is meant by "upper limit of work done on Earth"?
Replies
7
Views
1K
MHB Translate the statements into set inclusion
Replies
5
Views
1K

Hot Threads

Recent Insights

Back
Top