- #1
Thinkaholic
- 19
- 6
Hi! I know all of you might know what I'm about to post, but I just discovered it for myself, and I want to share my enthusiasm.
Let
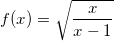
and
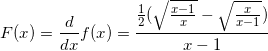 (here, I'll be restricting the domain of f(x) to the positive real numbers.)
(here, I'll be restricting the domain of f(x) to the positive real numbers.)
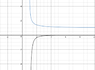
Here is a graph of the two, with f(x) in blue and F(x) in black:
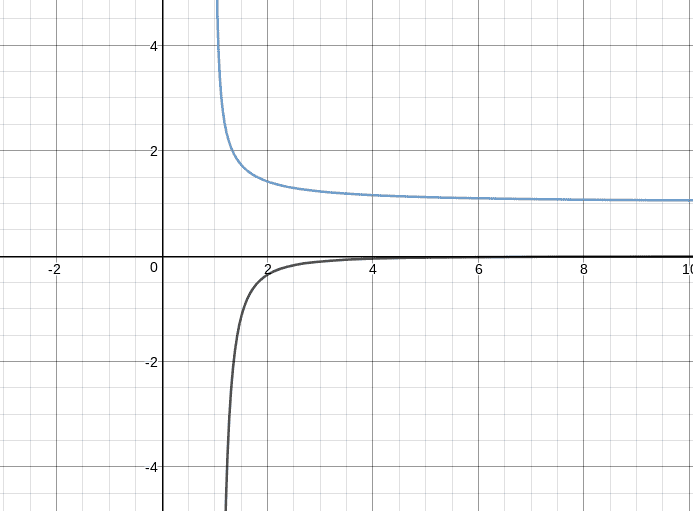
1st question: Where does f(x) intersect with the line y=x?
you could write
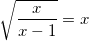
squaring both sides of the equation, multiplying both sides by x-1, and subtracting x from both sides gives
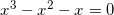
Factoring x from the LHS and dividing both sides by x leaves you with
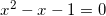
This is the minimal polynomial for the golden ratio, or φ, and the minimal polynomial for -φ^-1, or -Φ. This means that the quadratic above has two solutions at φ and -Φ. -Φ cannot be the solution we are looking for, as, as stated above, I am only dealing with f(x) within the domain of the positive real numbers (positive x values only). So, the intersection of f(x) and y=x is at (φ,φ)!
Question 2: What is the value of
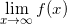 ?
?
Using L'Hospital's Rule, we obtain that
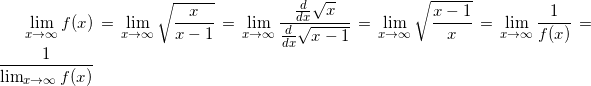
calling the limit as x approaches infinity of f(x) "L", then this becomes
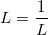
and obviously L=1. So
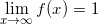 .
.
Question 3: What is the derivative of f(x) at (φ,φ)?
If we take the derivative of f(x), plug in φ for x, and make sure to remember that φ-1=Φ and that φ^-1=Φ, we simplify:
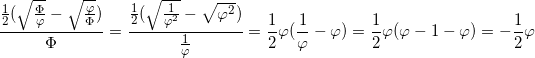 Question 4 (finale): What is
Question 4 (finale): What is
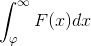 ?
?
From the fundamental theorem of calculus
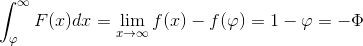
So we could rewrite this as:
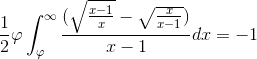 Hope I made no typos! Sorry if this is too long, but I want to share these interesting facts with y'all. Also, hopefully the type doesn't mess up, I used rendered LaTeX and pasted the images here. Also, the prefix is beginner, as most of the calculus stuff is taught in high school, but I really don't know what this is, so sorry if that is wrong.
Hope I made no typos! Sorry if this is too long, but I want to share these interesting facts with y'all. Also, hopefully the type doesn't mess up, I used rendered LaTeX and pasted the images here. Also, the prefix is beginner, as most of the calculus stuff is taught in high school, but I really don't know what this is, so sorry if that is wrong.
Let
and
Here is a graph of the two, with f(x) in blue and F(x) in black:
1st question: Where does f(x) intersect with the line y=x?
you could write
squaring both sides of the equation, multiplying both sides by x-1, and subtracting x from both sides gives
Factoring x from the LHS and dividing both sides by x leaves you with
This is the minimal polynomial for the golden ratio, or φ, and the minimal polynomial for -φ^-1, or -Φ. This means that the quadratic above has two solutions at φ and -Φ. -Φ cannot be the solution we are looking for, as, as stated above, I am only dealing with f(x) within the domain of the positive real numbers (positive x values only). So, the intersection of f(x) and y=x is at (φ,φ)!
Question 2: What is the value of
Using L'Hospital's Rule, we obtain that
calling the limit as x approaches infinity of f(x) "L", then this becomes
and obviously L=1. So
Question 3: What is the derivative of f(x) at (φ,φ)?
If we take the derivative of f(x), plug in φ for x, and make sure to remember that φ-1=Φ and that φ^-1=Φ, we simplify:
From the fundamental theorem of calculus
So we could rewrite this as:
Attachments
-
 upload_2018-5-9_19-1-12.png3.4 KB · Views: 433
upload_2018-5-9_19-1-12.png3.4 KB · Views: 433 -
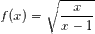 gif.gif560 bytes · Views: 751
gif.gif560 bytes · Views: 751 -
 gif.gif1.2 KB · Views: 646
gif.gif1.2 KB · Views: 646 -
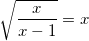 gif.gif423 bytes · Views: 438
gif.gif423 bytes · Views: 438 -
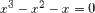 gif.gif351 bytes · Views: 434
gif.gif351 bytes · Views: 434 -
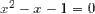 gif.gif323 bytes · Views: 426
gif.gif323 bytes · Views: 426 -
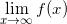 gif.gif467 bytes · Views: 425
gif.gif467 bytes · Views: 425 -
 gif.gif2.6 KB · Views: 421
gif.gif2.6 KB · Views: 421 -
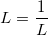 gif.gif248 bytes · Views: 433
gif.gif248 bytes · Views: 433 -
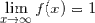 gif.gif520 bytes · Views: 430
gif.gif520 bytes · Views: 430 -
 gif.gif2.1 KB · Views: 422
gif.gif2.1 KB · Views: 422 -
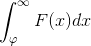 gif.gif623 bytes · Views: 416
gif.gif623 bytes · Views: 416 -
 gif.gif1.4 KB · Views: 426
gif.gif1.4 KB · Views: 426 -
 gif.gif1.2 KB · Views: 424
gif.gif1.2 KB · Views: 424
Last edited: