Space-intervals, proper time, and proper distance

[Stephanus]

Can I ask a question here?
What is proper distance?

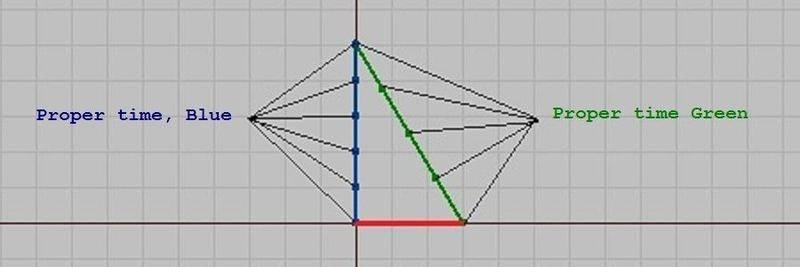
V = 0.6c

What is proper distance for Blue?
What is proper distance for Green?
Thanks.

 

[Nugatory]

We can always calculate the square of the spacetime interval between two events using $\Delta{s}^2=\Delta{t}^2-\Delta{x}^2$.

If $\Delta{s}^2$ is greater that zero, we call $\Delta{s}$ the "proper time" along the interval and say that the interval is "timelike". If it is less than zero, we call $\sqrt{-\Delta{s}^2}$ the "proper distance" along the interval and say that the interval is "spacelike".

In your example, both the blue and the green lines are timelike, so they have a proper time (five for the blue one, four for the green one) but no proper distance. The red line is spacelike and the proper distance along it is three.

 

[bcrowell]

Physically, proper distance is the length of an object as measured by an observer who is at rest relative to the object. The "object" doesn't actually have to be a physical object. If you have two events in spacetime, you can call them the ends of the "object," and then being at rest relative to the "object" means having a state of motion such that the two events are simultaneous.

 

[Stephanus]

Dear PF Forum,
I'm learning SR as a hobby.
And in these past 3 months, I have aquainted with some SR terms such as:
Proper time, world line, time like, space time diagram, light cone, event. Doppler effect, we were introduced in high school. And I find it important for me not to miss a single word, so that I can understand the post.
Here, I want to know about "Proper distance" (Btw, it took me 1 week to understand "Proper Time", it's the knot on the world line)

We can always calculate the square of the spacetime interval between two events using $\Delta{s}^2=\Delta{t}^2-\Delta{x}^2$.

Okay, if I'm not mistaken, we use this to calculate proper time.

If $\Delta{s}^2$ is greater that zero, we call $\Delta{s}$ the "proper time" along the interval and say that the interval is "timelike". If it is less than zero, we call $\sqrt{-\Delta{s}^2}$ the "proper distance" along the interval and say that the interval is "spacelike".

Yes, I understand this.

In your example, both the blue and the green lines are timelike

Are you trying to say that they don't have "proper distance"? I can understand it, if we look at the picture that I upload, We can boost the graph according to V, so that Red WL is at rest.
"How can a rest observer have distance?" It makes sense.
But supposed, the left world line is at London and the right world line is at Paris. Isn't the distance between London and Paris 200 miles?

The red line is spacelike and the proper distance along it is three.

Physically, proper distance is the length of an object as measured by an observer who is at rest relative to the object. The "object" doesn't actually have to be a physical object. If you have two events in spacetime, you can call them the ends of the "object," and then being at rest relative to the "object" means having a state of motion such that the two events are simultaneous.

Here I presented the graph:

To calculate "proper time" we have to boost the picture at -V.
But I think we can calculate it using $\sqrt{\Delta t^2 - \Delta x^2} \text{ or } \sqrt{\Delta t^2 - (\Delta tv)^2}$
And to calculate "Proper distance" do we have to boost the picture at imaginary V?
Here for event S, the supposed V is 1.667c.
So, when I boost it at 1.667c, we have picture 2. S and E0 is simultanous and we can calculate the "Proper distance"
So, here my questions:
1. Does time like events have "proper distance"?
2. Because if we boost it at -V, the distance is 0 (see Pic 2 Red WL), but London and Paris is still 200 miles, isn't it?
3. To calculate "proper distance" $Proper Distance = \sqrt{\Delta x^2 - \Delta t^2}$? Or to boost it, so it's simultaneous?
Thanks for any confirmation.

 

[Stephanus]

Add:
An after tought
A: If $\sqrt{t^2 - x^2}$ is real, then there is no $\sqrt{x^2 - t^2}$. Time like cannot have proper distance.
B: If $\sqrt{x^2 - t^2}$ is real, then $\sqrt{t^2 - x^2}$ is imaginary. Space like cannot have proper time.
Is this the simple conclusion?

 

[Nugatory]

Add:
An after tought
A: If $\sqrt{t^2 - x^2}$ is real, then there is no $\sqrt{x^2 - t^2}$. Time like cannot have proper distance.
B: If $\sqrt{x^2 - t^2}$ is real, then $\sqrt{t^2 - x^2}$ is imaginary. Space like cannot have proper time.
Is this the simple conclusion?

Pretty much yes (although it is a good practice to write these expressions as $\Delta{t}^2-\Delta{x}^2$ and $\Delta{x}^2-\Delta{t}^2$ instead - that makes it clear that we're working with the difference between two coordinate values, not the values of coordinates).

The other important thing to bear in mind is that $\sqrt{\Delta{t}^2-\Delta{x}^2}$ and $\sqrt{\Delta{x}^2-\Delta{t}^2}$ will always have the same value in all inertial frames, even though the values of $\Delta{t}$ and $\Delta{x}$ may be very different (You can see this by doing some algebra with the Lorentz transformations). It is because of this that they have physical significance.