- #36
ghwellsjr
Science Advisor
Gold Member
- 5,122
- 150
Jaumzaum's link shows an aborted attempt to combine the last two diagrams from the last post. Here I will show a better way to do this but they still have problems and they cannot show the paths of the message for both twins on the same diagram. First is the combined diagram in which Pam is always at rest and in which she is receiving the messages from Jim. Note that everything she sees is accurate:
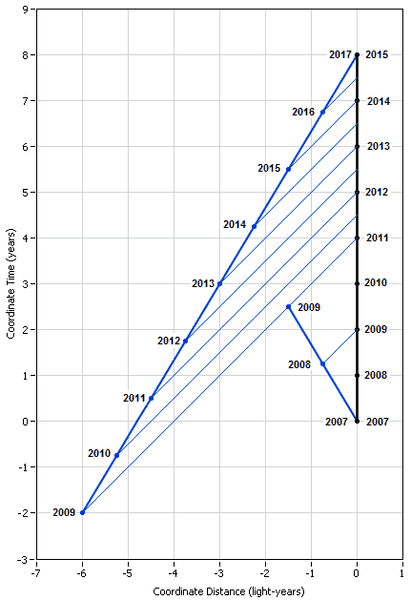
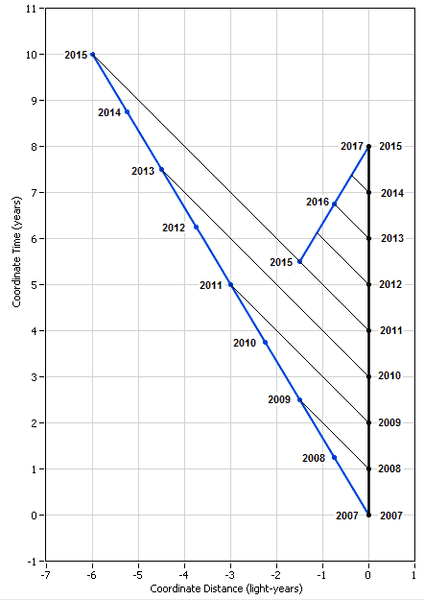
Next is the combined diagram in which Pam is always at rest and in which she is sending messages to Jim. Although it correctly shows when she sent the messages, she cannot tell the path they take to Jim.
This final non-inertial drawing in which Pam is always at rest correctly shows the timings for both Pam and Jim in terms of when they send and receive all the messages:
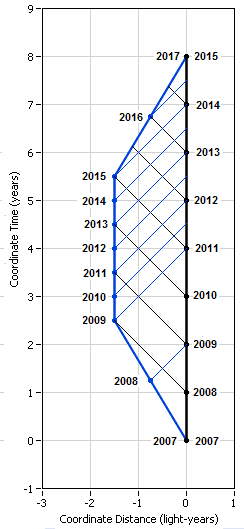
Note that Pam could always use a radar method to determine how far away Jim was and this diagram takes advantage of that information.
Next is the combined diagram in which Pam is always at rest and in which she is sending messages to Jim. Although it correctly shows when she sent the messages, she cannot tell the path they take to Jim.
This final non-inertial drawing in which Pam is always at rest correctly shows the timings for both Pam and Jim in terms of when they send and receive all the messages:
Note that Pam could always use a radar method to determine how far away Jim was and this diagram takes advantage of that information.
Attachments
Last edited:

