Special relativity and standard configuration

[greg997]

Homework Statement

Hi,
I am struggling to even start answering teh question as i fail to fully understand what is required.
So I got two planets, A and B. Both stationary. And a space ship which when passing by planet A sends a light pulse toward planet B. The space ship then continues its flight towards planet B at speed 0.5c. One clock on spaceship times sending pulse when at planet A, second clock on planet A times recives the signal, third clock times arrival of the light pulse at planet B. Also the third clock times arrival of space ship.The distance between planets is 20 light seconds.
1. list three events and determine position and time of three events in planets frame of reference

2.create a diagram showing planets frame of reference and the spaceships frame of reference when event 3-the light pulse arrives at planet B.
3. use lorentz transformation to transform all three events into spaceship's frame.

Relevant Equations

Lorenz equations

1. list three events and determine position and time of three events in planets frame of reference
I think the 3 events are:
E1- Spaceship is at planet A and sends the light pulse
E2 - light pulse arrives at planet B
E3- spaceships arrives at planet B

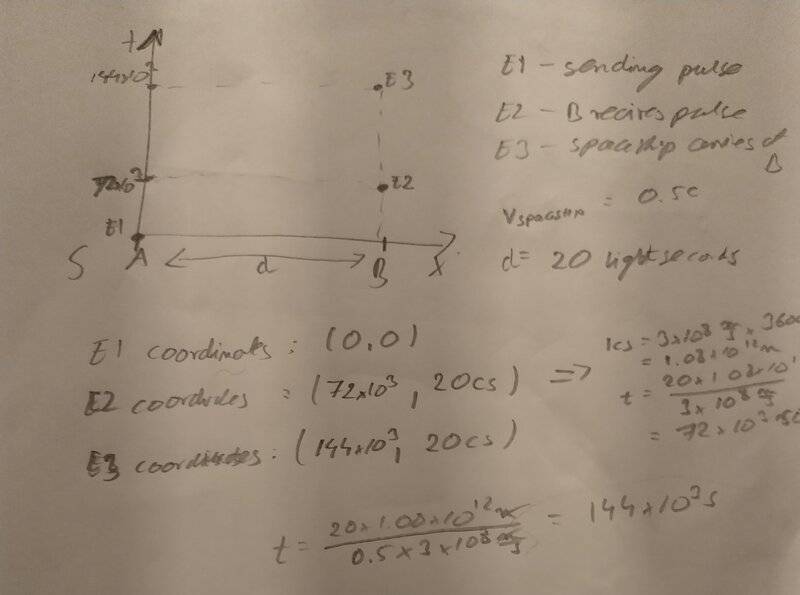
2.create a diagram showing planets frame of reference and the spaceships frame of reference when event -the light pulse arrives- at planet B.

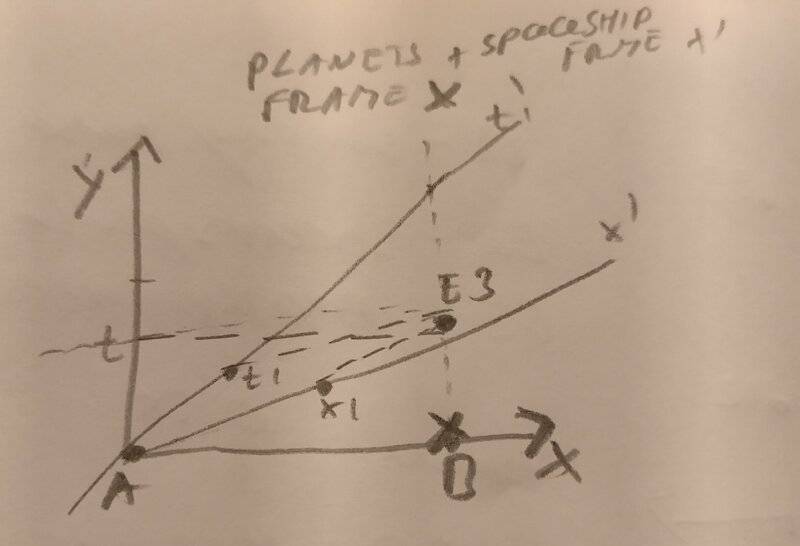
3. use lorentz transformation to transform all three events into spaceships frame.
The three coordinates are then transformed into spaceships frame of reference. Which i think is a matter of plugging in the data.

Do my calculations and diagrams make any sense at all? The second diagram with x' and t' is just guesswork.

 

[jbriggs444]

Let me concentrate on the event coordinates since I do not understand your diagrams.

I agree with the selection of events: $E_1$ for ship passing planet A and sending signal, $E_2$ for signal received at planet B and $E_3$ for ship passing planet B.

I agree with the $(0,0)$ coordinate for $E_1$. That is as good a place as any to place the origin for the coordinate system.

I do not understand $(72000,20c\text{s})$ for the coordinates for $E_2$.
I do not understand $(144000,20c\text{s})$ for the coodinates for $E_3$.

I assume that the first coordinate is for time and the second coordinate is for space and that $20c\text{s}$ stands for 20 light seconds. But what units are you using for time? Why not just use seconds for time?!

[If you are going to use units, use units consistently. Not light-seconds on one coordinate and then no units at all on another].

How much time does it take for a light signal to cover 20 light seconds?

Edit: I think I understand. You saw "20 light seconds" and somehow thought "20 light hours". It takes 72000 seconds for a light signal to traverse 20 light hours. It takes 144000 seconds for a ship moving at $0.5 c$ to traverse 20 light hours.

 

[greg997]

hi. thank you for your reply.

The distance between A and B is 20 ligt seconds , 20 cs.
The way i calculated the 72X10^3 is this.
1 cs = 3x10^8 m/s x 3600 s = 1.08x10^12m = that is distance unit but we got distance of 20cs so 20x 1.08x10^m
so time needed for the pulse to travel from A to B is t= (20x1.08x^12)/ speed of light( 3x10^8)= that gives me 72000 sec to travel taht distance 20 light seconds.
Does that make sense?
What about both diagrams?

 

[SammyS]

hi. thank you for your reply.

The distance between A and B is 20 light seconds , 20 cs.
The way i calculated the 72X10^3 is this.
1 cs = 3x10^8 m/s x 3600 s = 1.08x10^12m = that is distance unit but we got distance of 20cs so 20x 1.08x10^m
so time needed for the pulse to travel from A to B is t= (20x1.08x^12)/ speed of light( 3x10^8)= that gives me 72000 sec to travel taht distance 20 light seconds.
Does that make sense?

Your calculations verify what @jbriggs444 suspected. You are treating the distance from planet A to planet B as if it is given as 20 light hours, not 20 light seconds.

If light travels at a speed of $3.00 \times 10^8$ m/s, then how far does light travel in one second ?

 

[greg997]

it travels 2x10^m ..hmm
ok.. i see.
what about the frames of reference?
Are they correct? Is thai how they should look like for this scenario?

 

[Herman Trivilino]

Just leave the distances in light seconds and the times in seconds. That way c=1 and all the calculations are simpler.

 

[jbriggs444]

it travels 2x10^m

What in the world is $2 \times 10^m$?

 

[greg997]

it travels 2x10^m ..hmm
ok.. i see.
what about the frames of reference?
Are they correct? Is thai how they should look like for this scenario?

my mistake..it should be 3x10^8 m..ehh

 

[jbriggs444]

my mistake..it should be 3x10^8 m..ehh

So, what now should the coordinates be for the three events, $E_1$, $E_2$ and $E_3$ in the rest frame of the planets?

 

[greg997]

So, what now should the coordinates be for the three events, $E_1$, $E_2$ and $E_3$ in the rest frame of the planets?

are you saying that i should get time t= ( d/ v), which is then 20/ 3x10^8 for E2 and then 20/(0.5x3x10^8) for E3?

 

[jbriggs444]

are you saying that i should get time t= ( d/ v), which is then 20/ 3x10^8 for E2 and then 20/(0.5x3x10^8) for E3?

How much time does it take for a light pulse to travel 20 light-seconds?

If you have to use math to answer that question, you are not getting it.

 

[greg997]

20 seconds

 

[greg997]

so event e2 coordinates are ( 20cs, 20 ) ; ( x, t)?
i think i got my coordinates swapped in my handwritten attempt. it should be ( x, t) . correct?

 

[jbriggs444]

so event e2 coordinates are ( 20cs, 20 ) ; ( x, t)?
i think i got my coordinates swapped in my handwritten attempt. it should be ( x, t) . correct?

In my view, the coordinate order does not really matter as long as you are clear and consistent. Use whatever your teacher uses. Or whatever your textbook uses.

But yes, $E_2$ coordinates of $(20c\text{s}, 20\text{s})$ would be correct.

You have light-seconds as the units on distance. To be consistent, that means that the second coordinate value (time) should also have units (e.g. seconds) specified.

Can you show the coordinates for all three events?

 

[greg997]

In my view, the coordinate order does not really matter as long as you are clear and consistent. Use whatever your teacher uses. Or whatever your textbook uses.

But yes, $E_2$ coordinates of $(20c\text{s}, 20\text{s})$ would be correct.

As I read the "cs", that is $c$ for the speed of light and $\text{s}$ for a unit of seconds. So $20c\text{s}$ is 20 light-seconds as expected. However, to be consistent, that means that the second coordinate value (time) should also have units (seconds) specified.

Can you show the coordinates for all three events?

Thank you for that.
So I think the correct coordinates would be these
Ev1: (0,0)
Ev2: ( 20cs, 20s) arrival of light pulse at planet B.
Ev3: ( 20cs, 40s) arrival of spaceship at planet B at the speed of 0.5c.
Is that correct? And the reference frame of planets too? With the time axis t changed to new times as above?

 

[jbriggs444]

Ev1: (0,0)
Ev2: ( 20cs, 20s) arrival of light pulse at planet B.
Ev3: ( 20cs, 40s) arrival of spaceship at planet B at the speed of 0.5c.

Perfect.

Is that correct? And the reference frame of planets too? With the time axis t changed to new times as above?

The above coordinates are from a coordinate system in the rest frame of the planets.

Can you do a Lorentz transform of the three coordinate pairs to the reference frame of the ship?

 

[greg997]

Perfect.

The above coordinates are from a coordinate system in the rest frame of the planets.

Can you do a Lorentz transform of the three coordinate pairs to the reference frame of the ship?

I haven't tried yet but seems easy..t' and x' are found using these formulae.

For Ev1 event. The coordinates will be (0,0)
And for ev2 just plug in the values for v=c, and for X=20, for t=20.
But what do I get for ev 2 ? I get 0 in denominator.
No solution then?
Ev3. V= 0.5c , X=20 and t=40

 

[Herman Trivilino]

v=c

According to your first post, v = 0.5 c.

 

[greg997]

so i got following calculation for lorentz transformation

 

[greg997]

HAve i messed up calculations?
I am getting some negative values for both t'and x'. I dont understand the meaning of these.

 

[jbriggs444]

so i got following calculation for lorentz transformation
View attachment 340166

You have mis-quoted the Lorentz transform for time.

 

[greg997]

oo...x is missing. thank you. I will recalculate these

 

[greg997]

You have mis-quoted the Lorentz transform for time.

I think the solutions for events 2 and 3 are correct calculation wise. Are these correct? The times and position?
Why are positions negative? What is the meaning of these results?

 

[jbriggs444]

I think the solutions for events 2 and 3 are correct calculation wise. Are these correct? The times and position?
Why are positions negative? What is the meaning of these results?

You should avoid mixing units willy-nilly. In particular, consider what 20 light seconds minus 0.5 c times 40 seconds should yield.

Edit: fixed the numbers to match those from your images.

You should be using seconds and light-seconds as your only units. Forget you ever heard about meters or $3.0 \times 10^8$ meters/second.

 

[greg997]

hmm. very intresting.
so I get this 20cs -0.5c x 40s =? 20cs - 0.5x3x^8 m/s x40s so i get 20cs - 6x10^9 meters
from online convertors it says 20cs = 5995849x10^9 meters. How they got that number i do not know.
So would it be correct that 20cs -0.5c x 40s= (5995849x10^9 m)- (6x10^9m)=6x10^15 m ?

 

[jbriggs444]

hmm. very intresting.
so I get this 20cs -0.5c x 40s =? 20cs - 0.5x3x^8 m/s x40s so i get 20cs - 6x10^9 meters
from online convertors it says 20cs = 5995849x10^9 meters. How they got that number i do not know.
So would it be correct that 20cs -0.5c x 40s= (5995849x10^9 m)- (6x10^9m)=6x10^15 m ?

Forget you ever heard of meters. Forget you ever heard of online converters. It is way simpler than that.

How far does a rocket go in 40 seconds at 0.5 c. Express the answer in light-seconds.

 

[greg997]

20cs?
if the spped was 1c then it would travel 40 light seconds.

 

[jbriggs444]

20cs?
if the spped was 1c then it would travel 40 light seconds.

Right. So 20 light seconds minus 20 light seconds is what?

 

[greg997]

it is 0 of course. But then it means my x' for my event is 0. But what is the meaning of this?
From point of refrence of the spaceship the arrival at planet b is at position x'=0?
whta about t' for that event?
t'=t-vx/c^2/ denominator) ...40s-(0.5c x20cs)/c^2 is that c cancelled and i am left with 40s-10s= 30s/denominator ?

 

[jbriggs444]

it is 0 of course. But then it means my x' for my event is 0. But what is the meaning of this?

Event 3 is at x' coordinate zero in the rest frame of the ship. After all, the ship is right there at that event.

From point of refrence of the spaceship the arrival at planet b is at position x'=0?
whta about t' for that event?

$t'$ for event 3 is the elapsed time on the shipboard clock when the ship reaches event 3.

t'=t-vx/c^2/ denominator) ...20s-(0.5c x20cs)/c^2 is that c cancelled and i am left with 20s-10s= 10s/denominator ?

20s - (0.5c * 20s). That does not sound like a computation for $E_3$.