- #1
Alex Pavel
- 25
- 0
Good evening. I think I've got it as far as time dilation is concerned. Could someone please let me know if this calculation is correct?
- From frame C( stationary camera) Bob is moving at 50,000KM/second parallel to Alice's path
- Bob is also 50,000KM behind Alice on the parallel path
- Bob's path is 299,972 kilometers (1 light second) north of Alice's
- Knowing this, Alice knows that if she fires a laser bolt straight north, Bob will run into it.
- Alice fires the shot. Her camera (C) remains on the spot, facing North. She does not alter her vector
- When the bolt hits Bob, the camera records the time as one second after the shot is taken
- When the bolt hits Bob, Alice's clock shows 0.972 seconds since the shot
- Bob's clock also shows 0.972 seconds since the shot
- I put H (hypotenuse) in for reference but i do not think we need it, even though this is the path Alice 'sees'.
- Key issue is the camera sees path Y and it takes one second to reach the target in that frame.
- What does Alice's clock show if she triggered the shot at 0? Is it the same as Bob's?
Thanks!
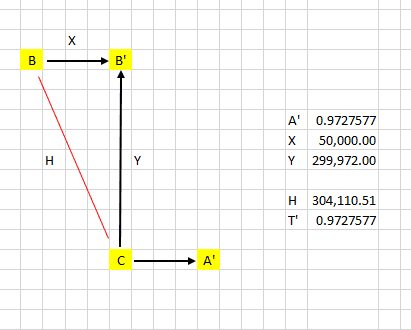
- From frame C( stationary camera) Bob is moving at 50,000KM/second parallel to Alice's path
- Bob is also 50,000KM behind Alice on the parallel path
- Bob's path is 299,972 kilometers (1 light second) north of Alice's
- Knowing this, Alice knows that if she fires a laser bolt straight north, Bob will run into it.
- Alice fires the shot. Her camera (C) remains on the spot, facing North. She does not alter her vector
- When the bolt hits Bob, the camera records the time as one second after the shot is taken
- When the bolt hits Bob, Alice's clock shows 0.972 seconds since the shot
- Bob's clock also shows 0.972 seconds since the shot
- I put H (hypotenuse) in for reference but i do not think we need it, even though this is the path Alice 'sees'.
- Key issue is the camera sees path Y and it takes one second to reach the target in that frame.
- What does Alice's clock show if she triggered the shot at 0? Is it the same as Bob's?
Thanks!


