- #1
Taxi1337
- 5
- 0
I am working on the same problem as a previous post, but he already marked it as answered and did not post a solution.
https://www.physicsforums.com/threads/sphere-with-non-uniform-charge-density.938117/
I am curious as to a method of finding the ##k## and substituting into the electric field. I tried this way.
$$ρ=\frac {k} {r}\,\,\,\,\,\,(1) $$
$$ρ=q \cdot (Volume)\,\,\,\,\,\,(2)$$
$$ρ=ρ\,\,\,\,\,\,\,(3)$$
$$\frac {k} {r}=q \cdot (Volume)\,\,\,\,\,\,(4)$$
$$k=q \cdot {(Volume)} \cdot r\,\,\,\,\,\,(5)$$
$$k=q \cdot {4 \pi r^2} \cdot r\,\,\,\,\,\,(6)$$
$$k=q \cdot {4 \pi r^3}\,\,\,\,\,\,(7)$$
then substitute ##k## from into ##E=\frac {k} {2 ε} \,\,\,\,\,\,(8)##
$$E_{inside}=\frac {q \cdot {4 \pi r^3}} {2 ε}\,\,\,\,\,\,(9)$$
Finally
$$E_{inside}=\frac {2 { \pi q}} {ε} r^3\,\,\,\,\,\,(10) $$
which goes like
$$E_{inside}= r^3\,\,\,\,\,\,(11) $$
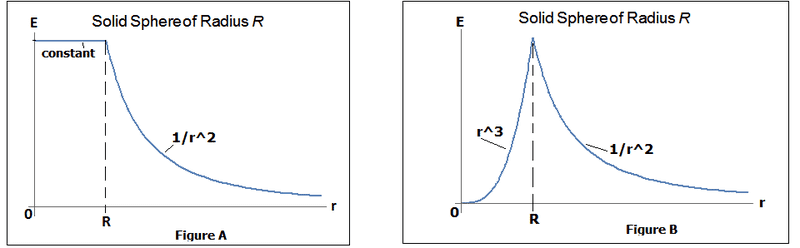
When I plot the electric field for the inside and outside I get ( i took all the constants as =1 for the graph)
for ##figure A## I plotted equation ##(8)## ( i took all the constants as =1 for the graph) so ##E=1##
for ##figure B## i plotted equation ##(11)##.
What is interesting to me is if I solve for ##k## and substitute into ##(8)## It makes a large difference in ##E_{inside}##. BUT when I solve for ##k## for the outside i still get an equation that goes like ##E_{outside}=\frac {1} {r^2}\,\,\,(12)##.
I found $$E_{outside}=\frac {k \cdot {4 R^2}} {2 ε r^2}\,\,(13)$$ and when I plug in ##k=q \cdot {4 \pi R^3}\,\,(14)## into ##(13)## i get $$E_{outside}=\frac {q \cdot {4 \pi R^3} \cdot {4 R^2}} {2 ε r^2}=\frac {q \cdot {\pi } \cdot {R^5}} {2 ε r^2}\,\,(15)$$
where in ##(15)## it still goes like ##\frac {1}{r^2}## no matter if i put in ##k## or not.
Thank you for your help, any input big or small is appreciated. It doesn't have to be elaborate.
Jared
https://www.physicsforums.com/threads/sphere-with-non-uniform-charge-density.938117/
Bonewheel said:
1. Homework Statement
A sphere of radius R carries charge Q. The distribution of the charge inside the sphere, however, is not homogeneous, but decreasing with the distance r from the center, so that ρ(r) = k/r.
1. Find k for given R and Q.
2. Using Gauss’s Law (differential or integral form), find the electric field E inside the sphere, i.e., for r < R.
Homework Equations
[tex]\int_V \rho \, dV = Q[/tex]
[tex]\oint \vec E \cdot d \vec A = \frac {Q_{enclosed}} {\epsilon_0}[/tex]
[tex]\vec {\nabla} \cdot \vec E = \frac {\rho} {{\epsilon}_0}[/tex]
The Attempt at a Solution
1. [tex]\int_V \rho \, dV = \int_{0}^{2 \pi} \int_{0}^{\pi} \int_{0}^R \frac k r r^2 \sin \theta \, dr \, d \theta \, d \phi = 2 k \pi R^2 = Q[/tex]
The units check out here.
2.
Here's where I ran into a problem. I tried using both the differential and integral forms of Gauss's Law, and in both cases the r canceled out, leaving me with an expression for the electric field I know is wrong. Oddly, the units work out here as well.
[tex]\oint \vec E \cdot d \vec A = 4 \pi r^2 E = \frac {Q_{enclosed}} {\epsilon_0} = \frac {2 k \pi r^2} {{\epsilon}_0} [/tex]
[tex]\vec {\nabla} \cdot \vec E = \frac 1 {r^2} \frac {\partial} {\partial r}(r^2 E_r)= \frac {\rho} {{\epsilon}_0} = \frac k {r {{\epsilon}_0}}[/tex]
[tex]E = \frac k {2{{\epsilon}_0}}[/tex]
Thank you so much for any help! Please let me know if you need any further information or edits for clarification.
I am curious as to a method of finding the ##k## and substituting into the electric field. I tried this way.
$$ρ=\frac {k} {r}\,\,\,\,\,\,(1) $$
$$ρ=q \cdot (Volume)\,\,\,\,\,\,(2)$$
$$ρ=ρ\,\,\,\,\,\,\,(3)$$
$$\frac {k} {r}=q \cdot (Volume)\,\,\,\,\,\,(4)$$
$$k=q \cdot {(Volume)} \cdot r\,\,\,\,\,\,(5)$$
$$k=q \cdot {4 \pi r^2} \cdot r\,\,\,\,\,\,(6)$$
$$k=q \cdot {4 \pi r^3}\,\,\,\,\,\,(7)$$
then substitute ##k## from into ##E=\frac {k} {2 ε} \,\,\,\,\,\,(8)##
$$E_{inside}=\frac {q \cdot {4 \pi r^3}} {2 ε}\,\,\,\,\,\,(9)$$
Finally
$$E_{inside}=\frac {2 { \pi q}} {ε} r^3\,\,\,\,\,\,(10) $$
which goes like
$$E_{inside}= r^3\,\,\,\,\,\,(11) $$
When I plot the electric field for the inside and outside I get ( i took all the constants as =1 for the graph)
for ##figure A## I plotted equation ##(8)## ( i took all the constants as =1 for the graph) so ##E=1##
for ##figure B## i plotted equation ##(11)##.
What is interesting to me is if I solve for ##k## and substitute into ##(8)## It makes a large difference in ##E_{inside}##. BUT when I solve for ##k## for the outside i still get an equation that goes like ##E_{outside}=\frac {1} {r^2}\,\,\,(12)##.
I found $$E_{outside}=\frac {k \cdot {4 R^2}} {2 ε r^2}\,\,(13)$$ and when I plug in ##k=q \cdot {4 \pi R^3}\,\,(14)## into ##(13)## i get $$E_{outside}=\frac {q \cdot {4 \pi R^3} \cdot {4 R^2}} {2 ε r^2}=\frac {q \cdot {\pi } \cdot {R^5}} {2 ε r^2}\,\,(15)$$
where in ##(15)## it still goes like ##\frac {1}{r^2}## no matter if i put in ##k## or not.
Thank you for your help, any input big or small is appreciated. It doesn't have to be elaborate.
Jared
