- #1
mathmari
Gold Member
MHB
- 5,049
- 7
Hey! 
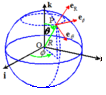
Using spherical coordinates and the orthonormal system of vectors $\overrightarrow{e}_{\rho}, \overrightarrow{e}_{\theta}, \overrightarrow{e}_{\phi}$
Could you give me some hints how I could do that?? (Wondering)
Using spherical coordinates and the orthonormal system of vectors $\overrightarrow{e}_{\rho}, \overrightarrow{e}_{\theta}, \overrightarrow{e}_{\phi}$
- describe each of the $\overrightarrow{e}_{\rho}$, $\overrightarrow{e}_{\theta}$ and $\overrightarrow{e}_{\phi}$ as a function of $\overrightarrow{i}, \overrightarrow{j}, \overrightarrow{k}$ and $(x, y, z)$ and
- calculate $\overrightarrow{e}_{\theta} \times \overrightarrow{j}$ and $\overrightarrow{e}_{\phi} \times \overrightarrow{j}$ with two ways: analytically, using (1), and geometrically.
Could you give me some hints how I could do that?? (Wondering)