Spherical Harmonics from operator analysis

[davidge]

I found an interesting thing when trying to derive the spherical harmonics of QM by doing what I describe below. I would like to know whether this can be considered a valid derivation or it was just a coincidence getting the correct result at the end.

Starting making a Fundamental Assumption that when dealing with the derivative operators, they will act only on their copies; e.g. $\partial_{\theta}$ acts only on $\partial_{\theta}$.

Knowing that

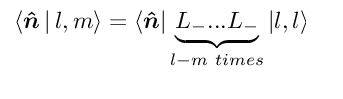
I got after working out

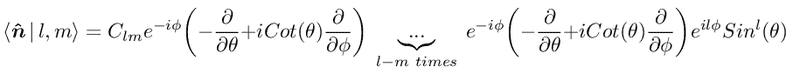
where $C_{lm}$ are the coefficients depending only on $l$ and $m$.

Now comes the crucial point. As by assumption each differential operator acts only on its copy, they will not act on the exponentials. Also, as there is nothing to differentiate w.r.t $\phi$, there will be no terms left with $\partial_\phi$. After working out the terms I got (with $u = Cos(\theta)$)

$$ C_{lm}\ e^{im \phi} \frac{\partial^{l - m}}{\partial u^{l - m}} \sqrt{1-u^2}^l \sqrt{1-u^2}^{\ - m} $$
Now, notice at this point I have worked out all the $(m-l)$ - $L_{-}$ operators. It is as if we were left only with ordinary quantities and therefore, I allowed the "once" differential operators to act on the functions.
If we can use ordinary product rule here, then we have (because the greatest order term for the second term on the right will be of order $|m|$ and the derivatives are of order $l-m$)

$$C_{lm}\ e^{im \phi} \frac{1}{\sqrt{1-u^2}^m} \frac{\partial^{l - m}}{\partial u^{l - m}} \sqrt{1-u^2}^l$$
as it should be.

If I'm wrong, then this was just a big coincidence!

 

[blue_leaf77]

Fundamental Assumption that when dealing with the derivative operators, they will act only on their copies; e.g. ∂θ\partial_{\theta} acts only on ∂θ

I am afraid that's not true. Anything that contains $\theta$ including the cotangent must be differentiated.

Also, as there is nothing to differentiate w.r.t ϕ\phi,

There is $e^{il\phi}$.

 

[vanhees71]

Indeed, an operator operates by definition on everything to the right!

 

[davidge]

Anything that contains $\theta$ including the cotangent must be differentiated.

The initial assumption excludes those terms.

There is $e^{il\phi}$.

By the initial assumption, it is just a constant for the operators.

Indeed, an operator operates by definition on everything to the right!

Exactly. That's why it bothers me to make the initial assumption that they will act only on equal operators.

blue_leaf77 and vanhees71,
I think the situation is more like a funny thing that happens when you modify a little bit the definitions.

 

[davidge]

Perhaps, more interesting is the fact that I got similar results, that is, I got the correct results in other areas of QM by using assumptions much like the one that I used for the derivation above.

Maybe am I not realising some property of the operators and thus I'm thinking my initial assumption does the work while in fact, there is another thing happening?

 

[blue_leaf77]

If I'm wrong, then this was just a big coincidence!

Can you give an example?

Maybe am I not realising some property of the operators and thus I'm thinking my initial assumption does the work

That's the most likely reason.

 

[vanhees71]

I don't really understand, what you did, but of course, when applying the "ladder operator" $\hat{L}_-$ succesively to $Y_l^{l}(\vartheta,\varphi)$ you have to differentiate all the dependencies on $\vartheta$ and $\varphi$ to get the correct spherical harmonics $Y_l^m$ for $m \in \{-l,-l+1,\ldots,l-1,l \}$. You can find the admittedly lengthy calculation in my QM FAQ (sorry for a German reference) here:

http://theory.gsi.de/~vanhees/faq/quant/node53.html

from Eq. (4.1.46) on.

 

[davidge]

Can you give an example?

Sorry, I'm not that good in English. What I mean is that if getting the correct result was an accident, then my "derivation" is not really a derivation.

You can find the admittedly lengthy calculation in my QM FAQ (sorry for a German reference)

Thanks. No need to be sorry.

After equation 4.1.71 you say that by iteration one obtains the expression for the $U_{lm} (u)$; you don't show how to do the iteration, though. Is it hard to do?

 

[vanhees71]

You just use the recursion relation (4.1.71) starting from (4.1.72). In the following paragraphs I give the proof for (4.1.73) by induction. It's not very difficult but a bit cumbersome to get all the factorials right. The merit of the method compared to the "traditional methods" is that you get these factors right by construction. I take this as an example for how much more transparent the abtract "Dirac formalism" can be compared to "wave mechanics". Of course, the latter methods you need very often for more complicated ("realistic") applications, where the symmetries of the problem are no longer sufficient to stick to the purely algebraic methods.

 

[davidge]

Just one more question, Is it okay to argue that the solutions $Y^{l}{}_{m}(\theta, \varphi)$ should be symmetric on $\varphi$ and thus we can choose a specific value of $\varphi$ when solving the differential equations satisfied by $Y^{l}{}_{m}(\theta, \varphi)$ in order to find it?

 

[vanhees71]

What do you mean by "symmetric in $\varphi$"? Since $Y_{lm}$ is the common eigenfunction of $\vec{L}^2$ and $L_z$, it's of the form
$$Y_{lm}(\theta,\varphi)=\Theta_{lm}(\theta) \exp(\mathrm{i} m \varphi).$$

 

[davidge]

What do you mean by "symmetric in $\varphi$"?

I mean the solution has the same form for any value of $\varphi$. Is it not so?

How does the statement

Since $Y_{lm}$ is the common eigenfunction of $\vec{L}^2$ and $L_z$

implies

it's of the form
$$Y_{lm}(\theta,\varphi)=\Theta_{lm}(\theta) \exp(\mathrm{i} m \varphi).$$

 

[vanhees71]

First you need the operators $\hat{L}_z$ and $\hat{\vec{L}}^2$ in position representation. Since (with $\hbar=1$)
$$\hat{\vec{L}}=-\mathrm{i} \vec{x} \times \vec{\nabla}$$
you just have to express $\vec{\nabla}$ in spherical coordinates:
$$\vec{\nabla}=\vec{e}_r \partial_r + \frac{\vec{e}_{\vartheta}}{r} \partial_{\vartheta} + \frac{\vec{e}_{\varphi}}{r \sin \vartheta} \partial_{\varphi}.$$
With $\vec{x}=r \vec{e}_r$ and the orthonormality of the spherical basis vectors, $\vec{e}_r \times \vec{e}_{\vartheta}=\vec{e}_{\varphi}$
you get
$$\hat{\vec{L}}=-\mathrm{i} \vec{r} \times \vec{\nabla} = -\mathrm{i} \vec{e}_{\varphi} \partial_{\vartheta} +\mathrm{i} \frac{\vec{e}_{\vartheta}}{\sin \vartheta} \partial_{\varphi}.$$
Since further $\vec{e}_z \cdot \vec{e}_{\varphi}=0$ and $\vec{e}_z \cdot \vec{e}_{\vartheta}=-\sin \vartheta$
$$\hat{L}_z=-\mathrm{i} \partial_{\varphi}.$$
This gives the eigenvalue equation
$$\hat{L}_z \mathrm{Y}_{lm}=-\mathrm{i} \partial_{\varphi} \mathrm{Y}_{lm}=m \mathrm{Y}_{lm}$$
with the solution
$$\mathrm{Y}_{lm}(\vartheta,\varphi)=\Theta_{lm} (\vartheta) \exp(\mathrm{i} m \varphi).$$
Since we want unique functions on the unit-sphere surface, we have necessarily $m \in \mathbb{Z}$.

For the somewhat more cumbersome calculation of $\hat{\vec{L}}^2$, see my QM manuscript (Eq. 4.1.46 ff),

http://theory.gsi.de/~vanhees/faq/quant/node53.html

or for printout

http://theory.gsi.de/~vanhees/faq-pdf/quant.pdf

 

[davidge]

Very good your explanation. Thank you.