Splitting Fields - Example 3 - D&F Section 13.4, pages 537 -

[Math Amateur]

I am reading Dummit and Foote, Chapter 13 - Field Theory.

I am currently studying Section 13.4 : Splitting Fields and Algebraic Closures ... ...

I need some help with an aspect of Example 3 of Section 13.4 ... ...

Example 3 reads as follows:

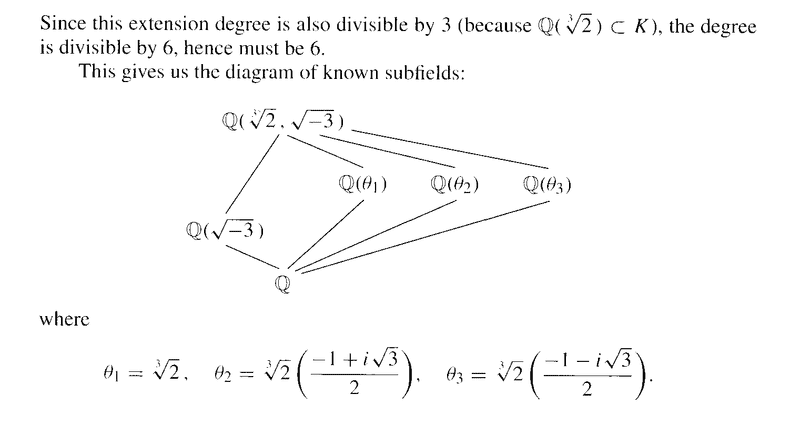
In the above text by Dummit and Foote, we read the following:

" ... ... Since $\sqrt{ -3 }$ satisfies the equation $x^2 + 3 = 0$ the degree of this extension over $\mathbb{Q} ( \sqrt [3] {2} )$ is at most $2$, hence must be $2$ since we observed above that $\mathbb{Q} ( \sqrt [3] {2} )$ is not the splitting field ... ... "I do not understand why the degree of the extension $K$ over $\mathbb{Q} ( \sqrt [3] {2} )$ must be exactly $2$ ... ... why does $\mathbb{Q} ( \sqrt [3] {2} )$ not being the splitting field ensure this ... ...

Can someone please give a simple and complete explanation ...

Hope someone can help ...

Peter

 

[andrewkirk]

The degree of any proper extension of a field must be at least two because the degree is the dimension of the extension considered as a vector space over the smaller field.

Given any nonzero vector in a finite-dimensional vector space, there exists a basis containing that vector. So we can take the 1 of the smaller field as the first vector in a basis for the extension. If no further vector is needed in the basis then the extension is identical to the original field. Hence the degree must be at least two for the extension to be proper.

Since it must also be no greater than two, it must be two.

 

[Math Amateur]

The degree of any proper extension of a field must be at least two because the degree is the dimension of the extension considered as a vector space over the smaller field.

Given any nonzero vector in a finite-dimensional vector space, there exists a basis containing that vector. So we can take the 1 of the smaller field as the first vector in a basis for the extension. If no further vector is needed in the basis then the extension is identical to the original field. Hence the degree must be at least two for the extension to be proper.

Since it must also be no greater than two, it must be two.

Thanks Andrew ... just now reflecting on what you have said ...

Peter