Splitting of a one-particle wave function

[Spacetime walker]

TL;DR Summary

A question about the possibility of separating a one-particle wave function by infinitely high potential walls.

Hello all, I am a newcomer here. Not a physicist, just an enthusiast. ;)

I was thinking whether it is possible to separate a one-particle wave function into two, "completely disjoint" parts. The following thought experiment explains better what I am thinking about.

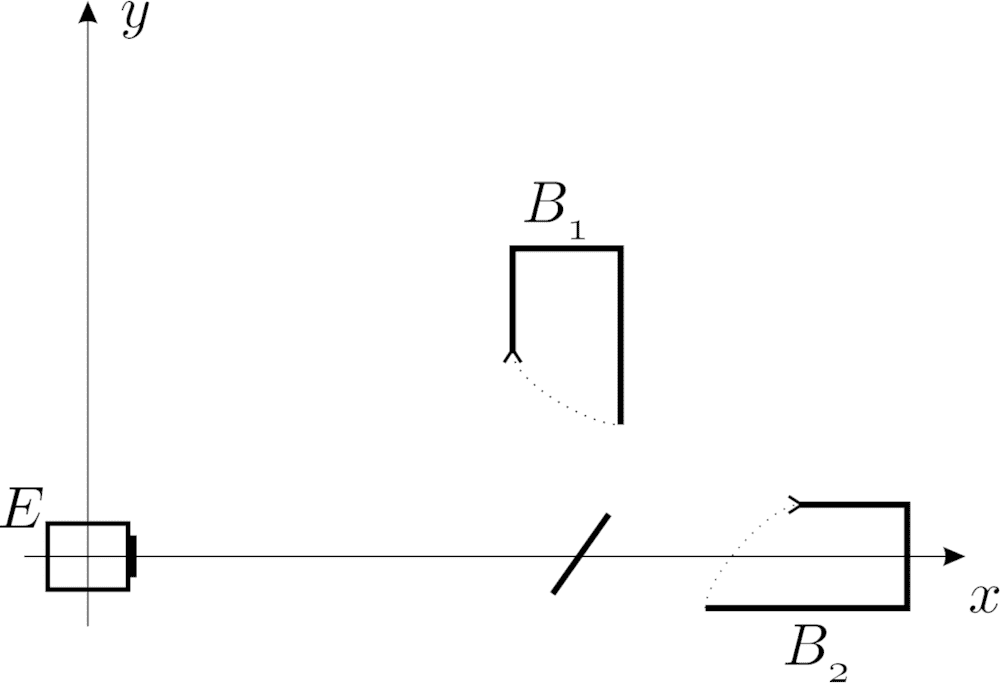
Let us suppose, that there is an emitter E in the origin of our coordinate system (see the below figure), and it emits an electron such that this electron moves in the x direction to the right (more realistically, its momentum points to the positive x direction with very high probability).

In some point on the right of the origin, there is a semi-transparent mirror rotated by 45 degrees. After the electron reaches this mirror, the wave function will have two peaks and these start to evolve in both directions (upwards, and to the right).

Suppose also that we have put a box in both of the possible electron-directions at some but equal distances from the mirror (B_1 and B_2 in the Figure). These boxes automatically close shortly after the electron is supposed to reach there (for this arrival time, you do not need to observe the electrons, it is enough to know the characteristics of the emitter, I think).

Thus, the boxes (like infinitely high potential walls) trap the wave function peaks. At the instance when the doors close, the wave function will completely be split into two parts without physical interaction possible. But still, we are talking about one particle.

My questions:
1) What I have written above was dictated by my intuition. Is this complete separation possible by the principles of QM?
2) And if it is possible, how can you explain the "spooky action at a distance" when you open one of the boxes at a later time if the box walls do not permit "communication" between the parts? (The wave function in the non-opened box must change instantaneously as well.)
Thank you for your answers, in advance! ;)

 

[PeroK]

Your set-up is, I think, just another example of an experiment where a particle can have one or more distinct eventual measurement outcomes. Like the Stern-Gerlach (with silver atoms).

The particle's wave function can evolve into a superposition of two or more spatially distinct components. Eventually, if you look for the particle you must get a measurement if it somewhere. In any case, in orthodox QM this entails the collapse of the wave-function. The extent to which the wave-function was previously spread across space or into distinct spatial components is not really an issue.

The theory of QM doesn't attempt to give any mechanism (or explanation) for how wave-function collapse occurs. QM merely specifies the probabilities of getting certain measurements of position.

 

[DrChinese]

Yes, there are a number of scenarios in which a quantum object might be "here" or "there" before "collapse" (whatever that is, which is generally interpretation dependent.

For example: a photon emitted from an excited atom could be considered to have a probability of being detected in a wide variety of spots (your "boxes"). When it is, all other boxes (regardless of distance) no longer may contain that particle.

Keep in mind that is true even if that box is so far away that the boxes could not all have been reached at the same time. I.e there is no requirement that "collapse" is something limited to a time interval related to the travel time to the point it was actually detected.

Is there a nonlocal effect being demonstrated? That is strictly interpretation dependent - much as it would be for entanglement effects. The results are always random, so no chance to send a signal.

 

[vanhees71]

Yes, there are a number of scenarios in which a quantum object might be "here" or "there" before "collapse" (whatever that is, which is generally interpretation dependent.

For example: a photon emitted from an excited atom could be considered to have a probability of being detected in a wide variety of spots (your "boxes"). When it is, all other boxes (regardless of distance) no longer may contain that particle.

Yes, and this is all of interpretation you need! There's a probability to detect a somehow prepared single photon by a detector put on any place (or you use an extended detector like a photo plate or a CCD cam) at any given time (after the photon has been prepared in a definite pure or mixed quantum state).

A single photon itself doesn't even have a well-defined position observable to begin with. All that makes sense when thinking about photons in the only adequate way to think about them, which is relativistic local QFT (or more specifically QED), are detection probabilities at a given location of the detector as a function of time.

 

[Spacetime walker]

What happens when the boxes are equipped with scales? I suppose that the scales will show zero difference, otherwise we could detect where the particle is. When our particle interacts with some of the atoms of either box, the momentum-exchange can be detected by the corresponding scale. Is this so?

Does not this mean that until the particle does not interact, it is, in some sense, nowhere? (In contrast of being "a bit everywhere".)

 

[PeterDonis]

I suppose that the scales will show zero difference, otherwise we could detect where the particle is.

Your apparatus does detect where the particle is: that's what the boxes do. For each run of your experiment, one and only one box will have an electron in it when the box doors close and the run is completed. You will be able to detect which box has the electron by any means which can distinguish whether an electron is present--a scale would work if it were accurate enough to detect a one-electron weight difference.

 

[Spacetime walker]

Your apparatus does detect where the particle is: that's what the boxes do. For each run of your experiment, one and only one box will have an electron in it when the box doors close and the run is completed. You will be able to detect which box has the electron by any means which can distinguish whether an electron is present--a scale would work if it were accurate enough to detect a one-electron weight difference.

Let me think: the boxes do not immediately cause the wave function collapse, because they are not equipped with detectors. *Before* the collapse and after the doors are closed, the wave function is split in two disjoint volumes, and we (or a scale) cannot tell where the particle is.
We can only tell where it is, and a scale can show the difference only when the particle interacts with one of the atoms of the box. This may not happen immediately but after some time.

 

[PeterDonis]

the boxes do not immediately cause the wave function collapse, because they are not equipped with detectors.

The boxes themselves are detectors; they interact with the electron and confine it. The fact that the experimenter neglects to put something on the boxes that he can actually read the output of is irrelevant.

*Before* the collapse and after the doors are closed, the wave function is split in two disjoint volumes, and we (or a scale) cannot tell where the particle is.

This is not correct. In terms of the modern method of analyzing such experiments, decoherence occurs as soon as the box doors are closed and the electron is confined within one or the other of the boxes. This means that "collapse" occurs as soon as the box doors are closed. Again, whether or not a human puts a device in place that can tell the human which box the electron is in is irrelevant; human detection of the result is not required for decoherence and "collapse" to occur.

 

[Spacetime walker]

This is not correct. In terms of the modern method of analyzing such experiments, decoherence occurs as soon as the box doors are closed and the electron is confined within one or the other of the boxes. This means that "collapse" occurs as soon as the box doors are closed.

I see. So when a particle is not in vacuum but there are some atoms around (the atoms of the boxes in this case), decoherence occurs? Or do you need some "cut" like when the boxes are shut?
I suppose that such a "cut" is necessary. Otherwise, we would contradict with the double-slit experiment. Namely, if a particle goes in a double-slit experiment, and meets with a slit (not a "cut"), it is not "measured" by one of the atoms of the slit. The wave-pattern behind the screen is visible.

 

[PeterDonis]

So when a particle is not in vacuum but there are some atoms around (the atoms of the boxes in this case), decoherence occurs?

In general it depends on the situation; you can't make a single blanket statement like this.

However, you specified that once the box doors are closed, the electron is confined. That means decoherence has to occur at that point. Whatever interaction between the box and the electron occurs, if it is enough to confine the electron in the box, is enough to make decoherence occur.

 

[StevieTNZ]

With decoherence, and to quote Jeffrey Bub, the electron is in an entangled pure state with the environment. Therefore, the electron is still in neither box.

 

[PeterDonis]

With decoherence, and to quote Jeffrey Bub, the electron is in an entangled pure state with the environment.

On a no collapse interpretation, yes. But discussions of interpretations belong in the interpretations forum, not here.

Therefore, the electron is still in neither box.

No, this is not correct even on a no collapse interpretation. On a no collapse interpretation, there is a branch of the wave function in which the electron is in one box, and a branch in which it is in the other box. There is no branch of the overall wave function in which the electron is not in a box.

 

[StevieTNZ]

No, this is not correct even on a no collapse interpretation. On a no collapse interpretation, there is a branch of the wave function in which the electron is in one box, and a branch in which it is in the other box. There is no branch of the overall wave function in which the electron is not in a box.

Correct. What I mean is in the classical sense, the electron isn't in either box.

Decoherence, as I understand it in ANY interpretation, is still an entanglement of the system with the environment.

 

[vanhees71]

Within the minimal interpretation all there is are the probabilities given by the formalism, i.e., in your case all that is certain is that the electron is in one of the boxes, and you only know probabilities to find it in either box. You can experimentally check this only by preparing many identical experimental setups (defining the preparation procedure of the electron, i.e., it's quantum state) and then look in which box the electron in each experiment are and count. The relative frequency you find the electron in a specific box should approach the predicted probability value when performing more and more experiments.

 

[PeterDonis]

What I mean is in the classical sense, the electron isn't in either box.

There is no "in the classical sense". We are talking about quantum mechanics. You might as well say that in the classical sense, atoms can't exist, so there can't be a box at all.

 

[PeterDonis]

Decoherence, as I understand it in ANY interpretation, is still an entanglement of the system with the environment.

Yes, that is correct. Where interpretations differ is what happens after that entanglement takes place.