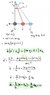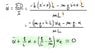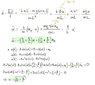Spring and string pendulum (oscillations)

[JulienB]

Homework Statement

Hi everyone! Here is a new problem about oscillations! Thx to all of you, I'm definitely making progress in the field. Let's see how that problem goes:

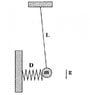
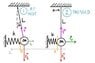
A pendulum of mass m is hanging on a string of length L and is "pushed" by a spring with spring constant k. At the deepest point of the pendulum (that is, when α = 0), the spring is compressed at x₀ of its equilibrium position.
a) determine the equation of motion of the angle α (for the case α<<1).
b) the solution of the equation is α(t) = A⋅sin(ω⋅t) + B⋅cos(ω⋅t) + α_R. Find the angular frequency and the angle α_R (equilibrium position) in terms of m, L, and k.
c) what is the solution, when the pendulum goes at t=0 from the position α = 0?

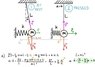
Check out the two attached picture. The 1st one describes the problem while the 2nd one shows my interpretation of the situation.

Homework Equations

Equation of motion, oscillations, torque

The Attempt at a Solution

a) At (2) (see pic), m⋅x'' = -k⋅x
⇔ x'' + (k/m)⋅x = 0

ΣD = F_F ⇒ α'' = -(k⋅x)/(m⋅L)

For a small angle we can say that (x/L) ≈ α, so the equation of motion goes:

α'' + (k/m)⋅α = 0

I'm pretty confident that it is correct, but let's see about b) :

I can input the solution to the equation in my equation for t=0, and after simplifying the cos and sin I get:

-B⋅ω² + (k/m)⋅B + (k/m)⋅α_R = 0

I do the same for α(0) and I find that α_R = 2⋅B. I input that in the previous equation and get, quite easily:

ω = √(3k/m)

Now I've tried a few things, mixing equations and states, but I can't get my hands on α_R! Could someone give me a clue in what direction I should look?

For c) I'm not sure I understand the question right. Isn't it what I have already done in B on the way of solving for ω?Thank you very much in advance for your advices, I appreciate it!Julien.

 

[drvrm]

A pendulum of mass m is hanging on a string of length L and is "pushed" by a spring with spring constant k. At the deepest point of the pendulum (that is, when α = 0), the spring is compressed at x0 of its equilibrium position.
a) determine the equation of motion of the angle α (for the case α<<1).
b) the solution of the equation is α(t) = A⋅sin(ω⋅t) + B⋅cos(ω⋅t) + αR. Find the angular frequency and the angle αR (equilibrium position) in terms of m, L, and k.
c) what is the solution, when the pendulum goes at t=0 from the position α = 0?

somehow i present a different picture- the initial condition given shows that the pendulum had come from some angular displacement and spent its entire energy in pushing the spring to a length x0 and now the spring will unwind and push the bob therefore the oscillation will continue with again the bob coming back and pushing the spring .
well in this situation at any instant of time t after the event if the displacement of the bob is alpha the two forces will act
1. the push by spring 2. the usual mgsin(alpha) and the equation of motion in angular coordinate will have these two terms. then its solution can be found.
if i am correct the new eq. will look different a term g/l will get added to -k/m term.

 

[JulienB]

@drvrm Mm that's interesting, I thought t=0 was when α=0 (that is, when whoever pressing the pendulum again the spring releases it into motion). I'll give some thoughts to your interpretation.

 

[drvrm]

whoever pressing the pendulum

your problem statement does not identify who is pushing and releasing it.
even an agency is there again at any angular displacement the mgsin alpha term will get added.

 

[haruspex]

somehow i present a different picture- the initial condition given shows that the pendulum had come from some angular displacement and spent its entire energy in pushing the spring to a length x0

I disagree. We are not told the initial state of motion.
At first, we are only told that when the string is vertical the spring is compressed x₀ from the equilibrium position (note, not 'to' a length x₀). We are not told a time or velocity corresponding to that position.
In part c, we are told to take it as being in the vertical position at t=0, but we still do not know the velocity at that time, so do not know the amplitude.
But I agree that gravity needs to be taken into account.

 

[JulienB]

But I agree that gravity needs to be taken into account.

Indeed otherwise the pendulum would not come back down right? I get back to it.

 

[JulienB]

Okay I've attached my new interpretation of the situation (it's actually very similar apart from dealing with g) and my calculations for a). I now get this equation of motion:

α'' - ((g/L) + (k/m))⋅α = 0

Is that correct? Then for b) I input the solution into the equation of motion and get:

-A⋅ω²⋅sin(ω⋅t) - B⋅ω²⋅cos(ω⋅t) - ((g/L) + (k/m))(A⋅cos(ω⋅t) + B⋅sin(ω⋅t) + α_R) = 0

I check out what happens for t=0 (is that allowed?? Is that the right way to proceed?) :

-B⋅ω² - ((g/L) + (k/m))(B + α_R) = 0
⇒ ω² = -((g/L) + (k/m))(1 + α_R/B)

I'm blocked here at the moment. I tried to find an expression for B in terms of α_R in the first and second derivatives of α(t), but I've been unsuccessful so far.

Julien.

 

[haruspex]

α'' - ((g/L) + (k/m))⋅α = 0

Your suspicions should be aroused immediately. According to that equation, the more alpha is positive the more its acceleration will be positive, leading to a runaway acceleration, not SHM. Check the signs.

 

[JulienB]

@haruspex I am really struggling. But those mistakes do help me to understand better what's going on there.
I have redone it and indeed get α'' + ((k/m) + (g/l))⋅α = 0. I input the solution in there and get:

A⋅sin(ω⋅t)⋅(ω² - ω₀²) + B⋅cos(ω⋅t)⋅(ω² - ω₀²) - ω₀²⋅α_R = 0
with ω₀ = √((k/m) + (g/l))

Then I rewrote the expression with ω = ω/ω₀ as I have observed some people do and I reach:

A⋅sin(ω⋅t)⋅(ω² - 1) + B⋅cos(ω⋅t)⋅(ω² - 1) - α_R = 0

If I set t = 0, this simplifies to:

ω² = 1 + α_R/B

Now (if that is -for once- correct), the ideal would be an equation with B and α_R allowing me to replace one or the other. α_R is only present in α(t), and for A to disappear t must be equal to zero. The only problem is that I don't know at which angle α the pendulum is going to be at that precise moment. Maybe there's another way.

I'm still working on the problem, but I wanted to update where I am standing now. Is that better, or is it still a disaster? Thank you very much again!Julien.

 

[JulienB]

I just had an idea to solve for ω. If I set up α(t) = 0, that means the pendulum is at its deepest point against the spring. Because it is the point where it changes direction, its velocity must also be 0, allowing me to use α'(t) = 0 as well. Is that valid?Julien.

 

[haruspex]

I just had an idea to solve for ω. If I set up α(t) = 0, that means the pendulum is at its deepest point against the spring. Because it is the point where it changes direction, its velocity must also be 0, allowing me to use α'(t) = 0 as well. Is that valid?
Julien.

No, when it says the deepest point it just means the lowest point in the swing. It does mot mean this is the extreme end of the swing.
I don't understand why you have both ω and ω₀. Your expression for ω₀ is the frequency, no?
In your equation

@haruspex
I have redone it and indeed get α'' + ((k/m) + (g/l))⋅α = 0

there is a term missing. Remember, the equilibrium position is not at alpha=0.
Suppose at the equilibrium position (α_R) the spring is compressed by x'. Write an equation about that.
When α=0, it is compressed a further x₀. Express the spring compression when at angle α in terms of L, α, x' and x₀.

 

[JulienB]

@haruspex Thank you for your patience, I don't know how you can stand all my mistakes. Okay now what about that:

At the equilibrium position the horizontal forces balances each other, thus m⋅g⋅sinα = -k⋅x'.

When α=0, only the spring force -k⋅(x' + x₀) acts horizontally, and I can derive from the torque the angular acceleration:

α'' = k⋅(x' + x₀)/(mL) = -(g/L)⋅sinα + (k/m)(x₀/L)
= -(g/L)⋅α - (k/m)⋅α_R

Every time I think I get something right it's wrong, so I'd better wait for a confirmation before going any further

Julien.

 

[haruspex]

m⋅g⋅sinα = -k⋅x'

Yes, except that should be α_R, and you can use the small angle approximation (I assume).

When α=0, only the spring force -k⋅(x' + x0) acts horizontally, and I can derive from the torque the angular acceleration:

I don't think we care specifically what the torque is at angle 0.

Express the spring compression when at angle α in terms of L, α, x' and x₀.

What I was looking for there was just a bit of geometry, nothing to do with forces or torques. From that, you can get the spring force in terms of those, and use the equilibrium equation to eliminate x'.

 

[JulienB]

@haruspex I've attached a picture of how I understood what you said. Hopefully this is correct. I get that -k⋅(x' + x₀) = (m⋅g - k⋅L)⋅α_R.

 

[haruspex]

@haruspex I've attached a picture of how I understood what you said. Hopefully this is correct. I get that -k⋅(x' + x₀) = (m⋅g - k⋅L)⋅α_R.

Not bad, but you have some sign errors. Since x is measured from the right, x' etc. are all positive. Mg sin α_R is positive too, so there should be no minus sign in that equation. Likewise, in the last equation both minus signs should be plus.

 

[JulienB]

@haruspex Okay, I've tried to repair the sign mistakes and to derive the equation of motion from that. I get α'' - (g/L)⋅(α + α_R) - (k/m)⋅α_R = 0. It looks a bit strange, not sure how to interpret it.

I've attached my calculation steps.

Julien.

 

[haruspex]

@haruspex Okay, I've tried to repair the sign mistakes and to derive the equation of motion from that. I get α'' - (g/L)⋅(α + α_R) - (k/m)⋅α_R = 0. It looks a bit strange, not sure how to interpret it.

I've attached my calculation steps.

Julien.

A couple of errors in your first $\ddot \alpha$ equation. As alpha increases, the gravitational force should act to reduce alpha, and the spring's tendency to increase alpha should reduce. So again some signs wrong.
Also, I don't understand the presence of x₀. This equation should be for a general position x, not the vertical position.

 

[JulienB]

@haruspex For the x₀ I was thinking x all along, I replaced it now. About the signs, I now get for the torque ∑τ = -k(x' + x)⋅L - m⋅g⋅sinα⋅L. I've attached the equation of motion.

Julien.

 

[JulienB]

I find dealing with the signs very confusing. When I will be finished with this problem (and that is apparently going to take a while), I'll post the whole solution again for people searching infos about the topic.

 

[haruspex]

@haruspex For the x₀ I was thinking x all along, I replaced it now. About the signs, I now get for the torque ∑τ = -k(x' + x)⋅L - m⋅g⋅sinα⋅L. I've attached the equation of motion.

Julien.

x is defined as the total compression. No need to add x₀ to that.
Also, you did not need to switch the sign on that term. Sorry if I gave you the impression you should. The spring force acts to the right, so tends to increase alpha. It's just that at larger alpha, that tendency is less.

 

[JulienB]

x is defined as the total compression. No need to add x₀ to that.

You mean I should just use -k⋅x instead of -k(x + x') in my torque?? I guess those are "equivalent" if x is defined as the total displacement. (I previously conceived x as the displacement between x' and the pendulum's position during the oscillation)

Also, you did not need to switch the sign on that term. Sorry if I gave you the impression you should. The spring force acts to the right, so tends to increase alpha. It's just that at larger alpha, that tendency is less.

If I understand well, you mean that once the mass has passed the equilibrium position on the right, the gravity will be acting in the other direction and make the pendulum fall back again? Then the torque would be k⋅x⋅L - m⋅g⋅sinα⋅L, right?

 

[haruspex]

You mean I should just use -k⋅x instead of -k(x + x') in my torque?? I guess those are "equivalent" if x is defined as the total displacement. (I previously conceived x as the displacement between x' and the pendulum's position during the oscillation)

Sure, you can define x how you like, as long as you are consistent.
With that, I agree with your first equation on the most recent attachment, except for the sign on the spring force term. The compression force tends to increase alpha.
But in the second equation, that spring force term has gone from variable (depending on x) to constant. There should be a reference to alpha in there.
I have $L\alpha_R=x_0$, $L\alpha=x_0-x$, $mg\alpha_R=x+x'$.
If you agree with those, use them to find an expression for x+x' in terms of $\alpha$ and $\alpha_R$.

 

[JulienB]

@haruspex Okay I tried again, but I'm a little unsure about one step. Would you mind looking again at my calculations?

 

[haruspex]

@haruspex Okay I tried again, but I'm a little unsure about one step. Would you mind looking again at my calculations?

Still one problem with a sign, right up front. As I wrote in post #20, the larger the value of x, the higher the acceleration of alpha. So what should the sign on kx be? When you propagate that through to the final equation, it will be right.

 

[JulienB]

@haruspex Hallelujah! Thank you so much! I still have to properly understand the behavior of F_F with the sign, but here are some new progress.

 

[haruspex]

@haruspex Hallelujah! Thank you so much! I still have to properly understand the behavior of F_F with the sign, but here are some new progress.

That's it!

 

[JulienB]

@haruspex that's amazing. One of my top three days ever. I've been crying for the past half hour, but it was tears of joy.

Unfortunately I'm afraid I'm stuck again with α_R. I've tried the Newton laws, to use the equations for α = α_R or α = 0 but I ran into circles, and it seems I cannot mix any of those equations together. Any tip? My exam is tomorrow, this problem is the last one I couldn't solve (and hopefully the exam won't be that hard since we barely started oscillations in class).

Thank you so much for all your help, I've redone a) again and understood why the signs are as they are.Julien.

 

[JulienB]

I still can't find α_R but I tried c):

If I understood them correctly, the conditions are:
α(0) = A⋅sin(ω⋅t) + B⋅cos(ω⋅t) + α_R = 0
α'(0) = A⋅ω⋅cos(ω⋅t) + B⋅ω⋅sin(ω⋅t) = 0
and the question isn't: what are A and B then?

I use the 2nd equation to transform the 1st one into:

B = -α_R⋅cos(ω⋅t)

and the 2nd one becomes:

A = -α_R⋅sin(ω⋅t)

Is that correct? If so, I'm only missing that α_R to complete the problem.Thank you so much.Julien.

 

[haruspex]

I still can't find α_R but I tried c):

If I understood them correctly, the conditions are:
α(0) = A⋅sin(ω⋅t) + B⋅cos(ω⋅t) + α_R = 0
α'(0) = A⋅ω⋅cos(ω⋅t) + B⋅ω⋅sin(ω⋅t) = 0
and the question isn't: what are A and B then?

I use the 2nd equation to transform the 1st one into:

B = -α_R⋅cos(ω⋅t)

and the 2nd one becomes:

A = -α_R⋅sin(ω⋅t)

Is that correct? If so, I'm only missing that α_R to complete the problem.Thank you so much.Julien.

Thought experiment: keep m, L and k the same, but change the relaxed length of the spring. α_R will change, yet none of the given facts is contradicted. Therefore you do not have enough information to find α_R.
One of my statements in post #5 was probably wrong. Reading the problem statement again, perhaps you are supposed to take it as being at rest at t=0. You seem to have assumed that already.

 

[JulienB]

@haruspex I imagine so since it was a problem at a real exam a couple of years ago. Well I read the problem again and nothing's stated about t=0 until question c) and it is unfortunately for α = 0 then.

 

[haruspex]

@haruspex I imagine so since it was a problem at a real exam a couple of years ago. Well I read the problem again and nothing's stated about t=0 until question c) and it is unfortunately for α = 0 then.

Yes, my remark about t=0 was only in relation to part c.
For part b, the only other suggestion I have is that it should say to find α_R in terms of m, L, k and x₀.

 

[JulienB]

Also, if I assume that α(0) = α_R, I think it implies that B = 0.

 

[JulienB]

Yes, my remark about t=0 was only in relation to part c.
For part b, the only other suggestion I have is that it should say to find α_R in terms of m, L, k and x₀.

Yes and that could be easily done with the force equation right? Well, thank you for your help in any case! Was my reasoning in part c) coherent?Julien

 

[haruspex]

Yes and that could be easily done with the force equation right? Well, thank you for your help in any case! Was my reasoning in part c) coherent?Julien

In the equation you posted for α'(0) you had a sign wrong, but that must have been a mistake in typing the post since the answer you got is right.