- #1
aspodkfpo
- 148
- 5
Poster has been reminded to post the Problem Statement and especially the Relevant Equations in schoolwork-type thread starts
- Homework Statement
- n/a
- Relevant Equations
- n/a
There is a trampoline drawn here and a graph of the spring force vs height.
I don't see why the spring force is decreasing at a decreasing rate with respect to height above trampoline.
F= kx = k * h/sin(theta), letting theta be between the horizontal and the spring.
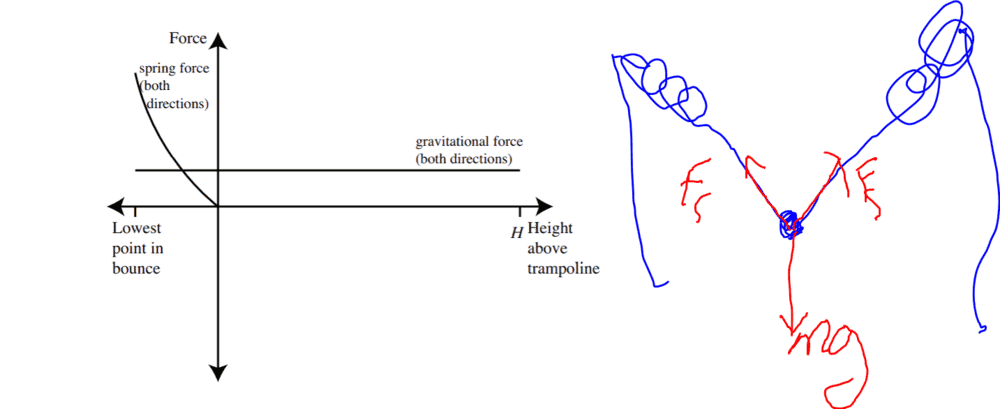
I don't see why the spring force is decreasing at a decreasing rate with respect to height above trampoline.
F= kx = k * h/sin(theta), letting theta be between the horizontal and the spring.
Last edited: