- #1
SqueeSpleen
- 141
- 5
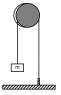
We have a mass M attached to a string.
In the other extreme of the string we have a spring.
We know the moment of inertia of the alloy I, and it's radius R.
We know the constant of the spring k.
The string is inextensible. String mass is negligible. There's not friction. There's no slipping. What's the frequence of the oscilation?
Attemp:
I know that the total energy in the system is:
[itex]U = h g m + \frac{1}{2} I \omega ^{2} + \frac{1}{2} k x^{2} [/itex]
As the string is inextensible, we have [itex]\Delta h = \Delta x \Leftrightarrow h-x = c[/itex]
Then, when h is at it's maximum x is at it's minimum. Also [itex]\omega = 0[/itex] at this time.
Then, by taking the following system of reference:
[itex]0 = h_{min}[/itex] and [itex]0 = x_{max}[/itex] we have that
[itex]x_{min} = -h_{max}[/itex]
[itex]\omega_{max}[/itex] is reached when [itex]h = \frac{h_{min}+h_{max}}{2} = \frac{h_{max}}{2}[/itex]. (Is this fine? How do I justify this? I'm guessing this movement is some of trigonometric function that's why I asserted that).
Then, as [itex]\nu = \frac{h_{max}-h_{min}}{4 \pi} \frac{1}{\omega_{max} R}[/itex]
Due to the fact that [itex](a sin(b t))'= ab \frac{\nu}{2 \pi} cos(b t)[/itex], then the maximum less the minimum of one, divided by the other gives us [itex]\nu[/itex]
Now, as in our system of references we have:
[itex]U = h g m[/itex] when [itex]h=h_{max}[/itex] and when [itex]h \frac{h_{max}}{2}[/itex] we have:
[itex]U = \frac{h_{max}}{2} g m + \big( \frac{1}{2} \frac{h_{max}}{2}\big) ^{2} k + \frac{1}{2} I \omega^{2}[/itex]
Then [itex]\frac{h_{max}}{2} gm - \big( \frac{1}{2} \frac{h_{max}}{2}\big)^{2} k = \frac{1}{2} I \omega^{2}[/itex]
[itex]\frac{h_{max}}{2} (gm-\frac{h_{max}}{4}) = \frac{1}{2} I \omega^{2}[/itex]
[itex]\sqrt{\frac{h_{max}}{I} (gm-\frac{h_{max}}{4})} = \omega [/itex]
Then
[itex]\nu = \dfrac{h_{max}}{4 \pi R \sqrt{\frac{h_{max}}{I} (gm-\frac{h_{max}}{4})} }[/itex]
I recently noticed that [itex] h_{max} [/itex] isn't given.
How do I deduct it?
PD: Forgive the bad drawing, I'm not very good with sketches.
In the other extreme of the string we have a spring.
We know the moment of inertia of the alloy I, and it's radius R.
We know the constant of the spring k.
The string is inextensible. String mass is negligible. There's not friction. There's no slipping. What's the frequence of the oscilation?
Attemp:
I know that the total energy in the system is:
[itex]U = h g m + \frac{1}{2} I \omega ^{2} + \frac{1}{2} k x^{2} [/itex]
As the string is inextensible, we have [itex]\Delta h = \Delta x \Leftrightarrow h-x = c[/itex]
Then, when h is at it's maximum x is at it's minimum. Also [itex]\omega = 0[/itex] at this time.
Then, by taking the following system of reference:
[itex]0 = h_{min}[/itex] and [itex]0 = x_{max}[/itex] we have that
[itex]x_{min} = -h_{max}[/itex]
[itex]\omega_{max}[/itex] is reached when [itex]h = \frac{h_{min}+h_{max}}{2} = \frac{h_{max}}{2}[/itex]. (Is this fine? How do I justify this? I'm guessing this movement is some of trigonometric function that's why I asserted that).
Then, as [itex]\nu = \frac{h_{max}-h_{min}}{4 \pi} \frac{1}{\omega_{max} R}[/itex]
Due to the fact that [itex](a sin(b t))'= ab \frac{\nu}{2 \pi} cos(b t)[/itex], then the maximum less the minimum of one, divided by the other gives us [itex]\nu[/itex]
Now, as in our system of references we have:
[itex]U = h g m[/itex] when [itex]h=h_{max}[/itex] and when [itex]h \frac{h_{max}}{2}[/itex] we have:
[itex]U = \frac{h_{max}}{2} g m + \big( \frac{1}{2} \frac{h_{max}}{2}\big) ^{2} k + \frac{1}{2} I \omega^{2}[/itex]
Then [itex]\frac{h_{max}}{2} gm - \big( \frac{1}{2} \frac{h_{max}}{2}\big)^{2} k = \frac{1}{2} I \omega^{2}[/itex]
[itex]\frac{h_{max}}{2} (gm-\frac{h_{max}}{4}) = \frac{1}{2} I \omega^{2}[/itex]
[itex]\sqrt{\frac{h_{max}}{I} (gm-\frac{h_{max}}{4})} = \omega [/itex]
Then
[itex]\nu = \dfrac{h_{max}}{4 \pi R \sqrt{\frac{h_{max}}{I} (gm-\frac{h_{max}}{4})} }[/itex]
I recently noticed that [itex] h_{max} [/itex] isn't given.
How do I deduct it?
PD: Forgive the bad drawing, I'm not very good with sketches.
Attachments
Last edited: