Springs and Pulleys - Force analysis

[Null_Void]

Homework Statement

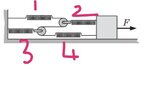
In the setup shown, a block is placed on a frictionless floor, the cords and pulleys are ideal and each spring has stiffness k. The block is pulled away from the wall. How far will the block shift, while the pulling force is gradually increased from zero to a value F

Pic below.

Relevant Equations

$F_s = Kx$

So I labelled all the springs from 1 to 4. Since the force is gradual, at equilibrium :

$F = k(x_2+ x_4) - - - - (1)$

Now we need to relate the different extensions of the springs:

$kx_1 = kx_4$ (same string)
$x_1 = x_4 (2)$
$kx_2 = 2kx_1$ ( ideal pulley)
$x_2 = 2x_1 (3)$

$kx_3 = 2kx_4$ (ideal pulley)
$x_3 = 2x_4$

Now I came to these equations by displacing each spring and assuming how much the pulleys would move. I'm not sure of how the string length would be distributed over the system.
I assumed that as spring-1 moves $x_1$ Half of this would be carried over to spring-2 and so on. I would like to know whether this is the right approach, and if so why?

Then I proceeded to equate $(1)$ with $(2)$ and $(3)$:

$F = k(3x_4)$
Thus,
$x_4 = F/3k$

Now this part is where I'm absolutely shaky:
Displacement of block $x = x_1/2 + x_2$

And so equating everything we get:

$x = 5{x_4}/2$

Therefore,

$x = 5F/6k$

But the given answer is ##10F/9k#

So where am I going wrong? And is there any way to easily deduce what would happen in such systems?

Thanks in Advance!

 

[haruspex]

Consider the three horizontal sections of string.
What is the relationship between the changes in lengths of the top and middle section and $x_1$ and $x_3$?

 

[Null_Void]

Consider the three horizontal sections of string.
What is the relationship between the changes in lengths of the top and middle section and $x_1$ and $x_3$?

The change in length of the top string is equal to the elongation of spring-1 while for the middle section it is equal to twice the elongation of spring-3

 

[Lnewqban]

Since the force is gradual, at equilibrium :

$F = k(x_2+ x_4) - - - - (1)$

I would say that equation 1 is not correct.

Please, see:
https://en.wikipedia.org/wiki/Series_and_parallel_springs

 

[haruspex]

I would say that equation 1 is not correct.

It is correct. Just consider the forces on the block.

The change in length of the top string is equal to the elongation of spring-1
while for the middle section it is equal to twice the elongation of spring-3

No, the pulleys will have moved.
Call those three length changes $y_1, y_2, y_3$.
What is the relationship between $x_1, y_1, x_2$ and $x$?
Similarly for $y_2, y_3$.

 

[Null_Void]

It is correct. Just consider the forces on the block.


No, the pulleys will have moved.
Call those three length changes $y_1, y_2, y_3$.
What is the relationship between $x_1, y_1, x_2$ and $x$?
Similarly for $y_2, y_3$.

$y_1 = - {x_1}/2$
$y_2 = +{x_1}/2 - 2x_3$
$y_3 = +2x_3$

I'm a bit confused about the displacement of the block. Since both the springs are connected to the block, I should get two equations for the same displacement $x$ right? One equation involving spring-1 and spring-2 and the other involving the rest. Is this the right approach?

 

[haruspex]

$y_1 = - {x_1}/2$
$y_2 = +{x_1}/2 - 2x_3$
$y_3 = +2x_3$

I don't know how you obtain any of those. I did mention that x should be in the equations.

Since both the springs are connected to the block, I should get two equations for the same displacement $x$ right? One equation involving spring-1 and spring-2 and the other involving the rest. Is this the right approach?

There are three. Follow through the three paths from end to the other. Each must add up to x.

 

[Null_Void]

I don't know how you obtain any of those. I did mention that x should be in the equations.

I assumed that the pulley moved a distance $l_1$, therefore the string must move $2l_1$ and thus this must also be equal to the spring's elongation:
$l_1 = {x_1}/2$
Displacement:
$x = l_1 + x_2$
$x = {x_1}/2 + x_2$
I'm still getting the same equation. Where am I going wrong?

For springs 3 and 4:
$x = 2x_3 + x_4$
I can't find the third equation you mentioned. I don't know how to account for the middle section and equate it to $x$

I can see that there will be changes to the lengths of the three sections, but I'm not sure about how to find a relation between them.

For section-1:
If spring 1 extends by $x_1$, string 1 should slack by $x_1$ and therefore the pulley must displace by ${x_1}/2$
Net change is $x_1$

Section-2:
From first pulley's extension, the length must increase by $x_1$ and if spring-3 expands by $x_3$ then net change is:
$x_1 - 2x_3$

For section-3:
$2x_3 + x_4$

Where have I gone wrong? Can you drop some more hints?

 

[Steve4Physics]

@Null_Void, it looks like you are at a bit of an impasse. You've clearly put some effort into this so I’d like to add a little to what @haruspex has already said.

In the simplified (and not to scale) diagram below, horizontal lines are horizontal string-sections; blue boxes are springs.

Working from left to right you should see that you can write three equations, the first being:
$\Delta PQ = \Delta PA + \Delta AB + \Delta BQ$.
(Using symbols from previous posts: $x= x_1 + y_1 + x_2$.)

See if you can write the other two similar equations. (Note that two of the three equations are effectively identical because of symmetry.)

Of course, since string length is constant, you have the additional equation:
$\Delta AB + \Delta BC + \Delta CD = 0$
(Using symbols from previous posts: $y_1+ y_2 + y_3 = 0$.)

The algebra is much simpler than it looks because you already know the value of extension for each spring (your Post #1).

 

[Null_Void]

@Null_Void, it looks like you are at a bit of an impasse. You've clearly put some effort into this so I’d like to add a little to what @haruspex has already said.

In the simplified (and not to scale) diagram below, horizontal lines are horizontal string-sections; blue boxes are springs.
View attachment 353687
Working from left to right you should see that you can write three equations, the first being:
$\Delta PQ = \Delta PA + \Delta AB + \Delta BQ$.
(Using symbols from previous posts: $x= x_1 + y_1 + x_2$.)

See if you can write the other two similar equations. (Note that two of the three equations are effectively identical because of symmetry.)

Of course, since string length is constant, you have the additional equation:
$\Delta AB + \Delta BC + \Delta CD = 0$
(Using symbols from previous posts: $y_1+ y_2 + y_3 = 0$.)

The algebra is much simpler than it looks because you already know the value of extension for each spring (your Post #1).

@Steve4Physics thanks for the post. I deeply appreciate it.

I now realise my mistake, I often avoided finding constraints by setting up coordinates and rather preferred to guess by cause and effect and that came back to bite me.

Like you said I found three equations, but I'm still not in the right.
I can clearly see the symmetry between path 1 and path 3, but I'm very doubtful about the change contributed by the pulleys

For path 1:
Spring-1 extension contributes $+x_1$ but string diminishes by $-x_1$ due to pulley but pulley also moves through $+{x_1}/2$ and spring-2 moves $x_2$
Therefore,

$x = {x_1}/2 + x_2$

For path-3:
Spring-3 extends by $x_3$ and thus pulley gives $+2x_3$ but pulley also covers $-x_3$ and finally we have $+x_4$.
Therefore,

$x = 2x_3 + x_4$

But clearly I'm the wrong, I know I properly haven't accounted for the pulley, but I don't exactly know where I went wrong. Can you point it out?
Also is it right If I consider the entire system to be fixed when calculating the length change over either pulley, i.e displacing spring by $x_1$ when the rest of the system is at rest and what consequently happens to $y_2$?
Also, Why won't springs-2 and 4 contribute to the displacement of the pulley (or do they?)

 

[Steve4Physics]

Hi @Null_Void, take a step back.

In post #1 you (correctly) found $x_4 = \frac F{3k}$. For neatness/conciseness, represent the quantity $\frac F{3k}$ by ‘$e$’.

First, express the values of $x_1, x_2, x_3$ and $x_4$ in terms of $e$. (Refer back to Post #1.)

Next, write out the ‘3 equations’ for the total extension ($x = \Delta PQ)$ as follows:
$x=$ some expression containing ‘$e$’sand ‘$y_1$’
$x=$ some expression containing ‘$e$’s and ‘$y_2$’
$x=$ some expression containing ‘$e$’s and ‘$y_3$’
Simplify these. Note the right hand sides of the 3 equations are equal (as they all equal $x$).

Remembering $y_1+ y_2+ y_3=0$ can you find $y_1, y_2$ and $y_3$ each in terms of $e$? Remember, length-changes can be positive or negative.

 

[Null_Void]

Hi @Null_Void, take a step back.

In post #1 you (correctly) found $x_4 = \frac F{3k}$. For neatness/conciseness, represent the quantity $\frac F{3k}$ by ‘$e$’.

First, express the values of $x_1, x_2, x_3$ and $x_4$ in terms of $e$. (Refer back to Post #1.)

Next, write out the ‘3 equations’ for the total extension ($x = \Delta PQ)$ as follows:
$x=$ some expression containing ‘$e$’sand ‘$y_1$’
$x=$ some expression containing ‘$e$’s and ‘$y_2$’
$x=$ some expression containing ‘$e$’s and ‘$y_3$’
Simplify these. Note the right hand sides of the 3 equations are equal (as they all equal $x$).

Remembering $y_1+ y_2+ y_3=0$ can you find $y_1, y_2$ and $y_3$ each in terms of $e$? Remember, length-changes can be positive or negative.

I'm extremely sorry that you had to spoonfeed me. The entire time I was trying to get at something else. Nevertheless huge thanks to you and @haruspex. I never would have guessed it would come down to solving linear equations. If you don't mind me asking could you tell me whether my approach is feasible? And could you explain your initial thought process when you first saw the question?

Again, huge thanks for your help!

 

[Steve4Physics]

If you don't mind me asking could you tell me whether my approach is feasible? And could you explain your initial thought process when you first saw the question?

Before attempting to answer those (very difficult!) questions, can you show us how you finally solved the problem?

[minor edit made.]

 

[Null_Void]

Before attempting to answer those (very difficult!) questions, can you show us how you finally solved the problem?

[minor edit made.]

Writing all the elongations in terms of e:
$x_1 = e$
$x_2 = 2e$
$x_3 = 2e$
$x_4 = e$

So like you pointed out, we get three equations:
$x = x_1 + y_1 + x_2$
$x = 3e + y_1$

$x = x_2 + y_2 + x_3$
$x = 4e + y_2$

$x = x_3 + y_3 + x_4$
$x = 3e + y_3$

$y_1 + y_2 + y_3 = 0$

We have four equations and four unknowns, this solving these equations gives us the answer ##x = 10e/3 .
I like how this method gets rid of the entire need to think about the pulley, thus making it much more simple.

 

[Steve4Physics]

We have four equations and four unknowns, this solving these equations gives us the answer ##x = 10e/3 .

Yes. But it doesn't look like you've actually done the working for yourself!

Because of the symmetry, the equations greatly simplify since $y _1 = y_3$ (can you see this?) Make sure you solve the problem to completion.

I like how this method gets rid of the entire need to think about the pulley, thus making it much more simple.

$y_2$ is the distance between the pulleys. So use of $y_2$ is thinking about the pulleys!

 

[Null_Void]

But it doesn't look like you've actually done the working for yourself

No, I actually did the working myself and only then posted my response. Even if you posted the direct answer, I would still try to work it out to see where it came from.

Because of the symmetry, the equations greatly simplify since y1=y3 (can you see this?

I noticed that the equations were symmetrical, but now that you mention it, I didn't use this result when I first solved it, though I should have.

y2 is the distance between the pulleys. So use of y2 is thinking about the pulleys!

But I never explicitly needed to find the relationship between the pulley's displacement and the string sections. That's what I meant.

 

[Null_Void]

Before attempting to answer those (very difficult!) questions, can you show us how you finally solved the problem?

[minor edit made.]

Could you tell your thought process initially?

 

[Steve4Physics]

If you don't mind me asking could you tell me whether my approach is feasible?

In this particular problem you started well by finding the extensions of the springs. But then there were some problems.

I think the problems arose because you ignored the fact that the distance between the pulleys must change to maintain a constant total string length. I don't think your approach could easily incorporate this because the length-changes are interrelated in a not-easy-to-see way (well, for me anyway).

And could you explain your initial thought process when you first saw the question?

Something like this...

a) Realised that it was easy to work out spring extensions as they aren’t affected by string lengths. They turn out to be $e = \frac F{3k}$ or $2e = \frac {2F}{3k}$ as you found in Post #1.

b) Worried a bit about how to deal with changes in the separation of the pulleys.

c) Drew a diagram in a simplified form (i.e. the one in Post #9) and marked length-changes on the diagram. To quote my old physics teacher: “Always draw a diagram.”.

d) Saw that if the top string’s length changes by $\Delta L$, so must the bottom string’s length. And as a result, the middle string’s length changes by $-2\Delta L$.

e)Looking at the diagram, noted that the change in the top (or bottom) path length must equal the change in the middle path length giving $e + \Delta L + 2e = 2e -2\Delta L + 2e$. Voila!

My general advice would be to get as much practice as possible and always draw a diagram!

 

[Null_Void]

Thank You very much for providing valuable insight. I deeply appreciate your post. Thanks a lot again!