Grasshopper said:
Could we maybe go into detail about why measurements at a distance require sychronizarion conventions
Say you are in New York and I am in Los Angeles. You send me a light signal. We want to figure out how long it took the signal to get from you to me. You measure the time by your clock when you emit the signal, and I measure the time by my clock when I receive the signal. In order for us to say that the difference between those times is the time it took the signal to travel, we have to assume that when your clock and my clock read the same time, those events are simultaneous--they happen at the same time. That is assuming a synchronization convention. (Note that we are both at rest relative to each other so there is no issue of relative motion affecting the
rates of our clocks; both clocks run at the same rate. The issue is solely how we define which events at the two clocks are simultaneous.)
Of course the convention I just described seems natural and obvious (assuming that we have previously undergone a procedure like Einstein clock synchronization to initialize both clocks in a way that matches the convention). But that doesn't mean it isn't a convention. Also, it is actually only natural and obvious if both clocks are at rest
in a global inertial frame. And that never actually happens in our actual universe, because spacetime in our actual universe is not flat, and because objects in our actual universe, like the Earth, do things like rotate on their axis. In a rotating frame, like the actual "rest frame" of the actual rotating Earth, Einstein clock synchronization
does not work globally. So any
actual clock synchronization between an actual clock in New York and an actual clock in Los Angeles
cannot be Einstein clock synchronization and
cannot satisfy all the properties of clocks synchronized that way at rest in a global inertial frame. We can use a
local inertial frame as an approximation, but it's just an approximation and is only useful in limited circumstances.
For an example of a different synchronization convention, consider GPS. The GPS system, roughly speaking, uses two
different reference frames. For the underlying clock synchronization and base calculations, it uses an Earth Centered Inertial (ECI) frame, which is an inertial frame whose spatial origin is the center of the Earth but which is not rotating with the Earth, and which defines clock synchronization using this non-rotating frame. (It also adjusts the clock
rate in this frame to match the actual clock rate on the Earth's geoid--roughly speaking, at "mean sea level" on an imaginary Earth that is covered entirely by ocean; such a mean sea level is an equipotential surface, i.e., it has the same clock rate everywhere on it.) But to actually display results to the user, it uses an Earth Centered Earth Fixed (ECEF) frame, which of course must be rotating with the Earth, but whose clock synchronization and clock rate is the same as the ECI frame. In other words, roughly speaking, it has the clock synchronization and time coordinate of the ECI frame, but spatial coordinates which are fixed to the rotating Earth. So both frames have the same clock synchronization, and it is not a "natural and obvious" one for observers on the rotating Earth (but it is for imaginary observers not rotating with the Earth but traveling in the same orbit about the Sun).
Grasshopper said:
why that presents a problem
It doesn't present a problem in many circumstances. GPS works fine with the conventions I described above.[
But it does present a problem if you're trying to understand the fundamentals of relativity with a light clock, because understanding the fundamentals means understanding the invariants--the things that
don't depend on any choice of convention. To do that, you have to eliminate anything from your scenario that
does depend on a choice of convention. That's why the light clock is defined with the emission and detection of the light pulse at the same place, and one "tick" of the clock corresponds to one round trip from emission, bouncing off the mirror, back to detection at the same place.
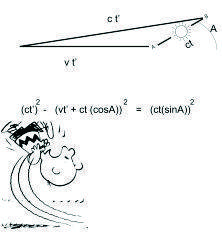
 The distance traveled by this photon in a given time, t, is c t
The distance traveled by this photon in a given time, t, is c t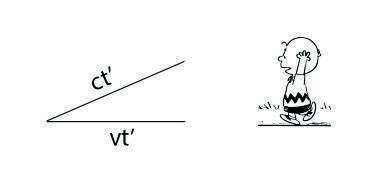
 And this allows the derivation of the equation.
And this allows the derivation of the equation. 
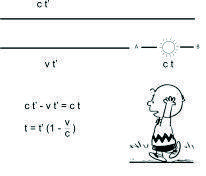 And so he gets a different equation.Yet a third passenger sets things up differently again.
And so he gets a different equation.Yet a third passenger sets things up differently again.