- #1
Est120
- 54
- 3
I am struggling to understand Callen's explanation for stability, I understand that the concavity of S(U) must be negative because otherwise we can show that this means that the temperature increases as the internal energy decreases (dT/dU<0) but I cannot understand equation (8.1) which basically says that the entropy must decrease and if the system is isolated that is absurd, in addition to what it refers to with "internal inhomogeneities"
the worst thing is that the text says that it is evident, it is geometrically clear, but what physical meaning does a final entropy resulting less than the initial one have? imagining 2 bodies isolated from the outside
I honestly believe that only the author understood that book
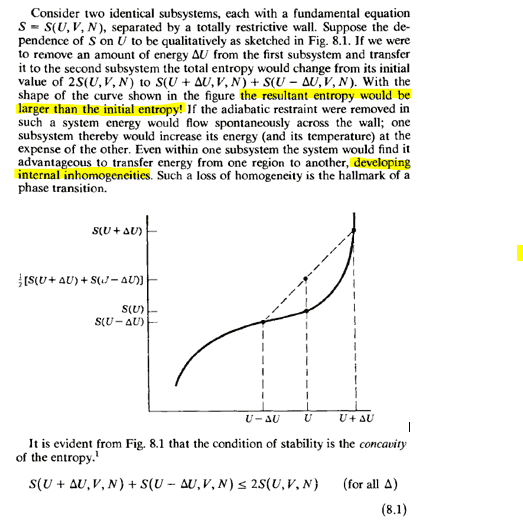
the worst thing is that the text says that it is evident, it is geometrically clear, but what physical meaning does a final entropy resulting less than the initial one have? imagining 2 bodies isolated from the outside
I honestly believe that only the author understood that book