Star Delta Transformation Proof

[GPhab]

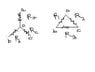
I've come across a proof for star-delta transformation which goes like this.(Refer to the diagram for notation. Pardon me for my bad drawing skills.)

In the delta, he found the effective resistance between two vertices ( say a and c, which can found easily). Then he found the effective resistance between the same two vertices (a and c)
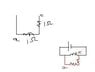
in the star. According to him R_ac in the star(which denotes the resistance between a and c) is equal to R_a + R_c. What about R_b? It might not be connected here but it may in a circuit. It is like this(refer to second attachment). The resistance about ac in the left diagram of second attachment is 2$$\Omega$$(drawing analogy from the "faulty" proof) but link it to another circuit (shown in right diagram), the resistance about ac is different. So just because it isn't connected, it doesn't mean that you can ignore it. Here's the surprise. The proof gives the CORRECT EQUATIONS. Work it out. You'll end up with the right thing!Can anybody make things clear for me?

 

[GPhab]

Did I not follow any guidelines? How come nobody is replying?

 

[weejee]

I wonder why the third line in your second diagram is connected directly to 'a' and not between 'a' and 'c'.

 

[rbj]

Did I not follow any guidelines? How come nobody is replying?

you need to be more patient. i hadn't seen this post before this moment. give it a couple of days and if no one responds by 48 hours, then you have good reason to inquire.


okay, first of all, this is normally called a "delta-Y transformation" or, less often, a "$\pi$-T transformation". never heard of the "Y" called a "star" in this context.

... R_ac in the star(which denotes the resistance between a and c) is equal to R_a + R_c. What about R_b? It might not be connected here but it may in a circuit.

if it's not connected to anything, no current flows through it. if no current flows through it, the behavior is no different than an open circuit (a.k.a. nothing).

So just because it isn't connected, it doesn't mean that you can ignore it. Here's the surprise. The proof gives the CORRECT EQUATIONS. Work it out. You'll end up with the right thing!Can anybody make things clear for me?

if the impedance (or any two-terminal part) isn't connected on one end, how does it make any difference if it's connected (or not) on the other end?

this "proof" you see is standard in any first-semester electrical engineering text (and i can go through it in detail if you want). the result is true, but i have never been satisfied with the proof because usually it requires assuming at the outset that the transformation of the circuit with all three terminals connected is equivalent to the transformation of the circuit when any arbitrary pair of terminals are connected. it turns out to be true for linear components (resistors or complex impedances) where the super-position property is valid (and that fact has to be established), but is not true for non-linear devices.

 

[berkeman]

Since this is homework/coursework, I moved it from General Physics to Homework Help.

 

[GPhab]

. it turns out to be true for linear components (resistors or complex impedances) where the super-position property is valid (and that fact has to be established), but is not true for non-linear devices.

Can it be established using the principles we learn in high school physics? (Actually this "Y-delta" transformation is not in our syllabus, but I picked it up so that I could get a convincing solution for some problems like a cube of resistors-It turned out to be one heck of a workout though. )

I haven't received a convincing reply for the contradiction we are facing in circuit2.

 

[Ram_1]

In the second image, R_ac will still be given by R_a+R_c.

The right hand circuit has an extra resistor (R₁) and as such the overall resistance of the circuit will be calculated using a different equation (this doesn't have any effect on R_ac only on the TOTAL resistance of the circuit). As the resistor R₁ in in parallel with the R_ac this would be calculated either using the product over sum rule:

$$R_{T}=\frac{R_{ac}\times R_{1}}{R_{ac}+R_{1}}$$

or the equation:

$$\frac{1}{R_{T}}=\frac{1}{R_{ac}}+\frac{1}{R_{1}}$$

I have attached a picture that will hopefully clarify my point a little further.

I think it is important to note that the circuits shown in the second image are in face connected in Star formation, if it were in Delta then there would only be a single Resistor connecting node A to node C (using the notation from your first diagram this would be R₂.)

In addition to what rjb was saying in relation to R_b when finding the value for R_ac, R_b has no effect but obviously when you come to find the value for R_ab and R_bc then R_b comes into effect.

again using notation from your first diagram:

$$R_{1}=R_{ab}=R_{a}+R_{b}$$

$$R_{3}=R_{bc}=R_{b}+R_{c}$$

I hope this helps

Ram