- #1
Dawei
- 30
- 0
Hello,
I'm trying to make sure I understand the basics of statistical mechanics and microstates/macrostates.
Being the nerd that I am, I have attempted to draw a diagram, as if I were explaining it to someone. If some one who is familiar with this topic could please review it and tell me if they see anything at all wrong, I would very much appreciate it.
The two systems are each two state systems, and to keep things simple I used the common "coin" analogy, where the total number of coins represents the total number of particles, and if they are "heads" then that means they are in the upper energy state. The two individual subsystems, as well as the final combined system, are all assumed to be completely closed. The only energy exchange allowed is between the two subsystems after they are in contact.
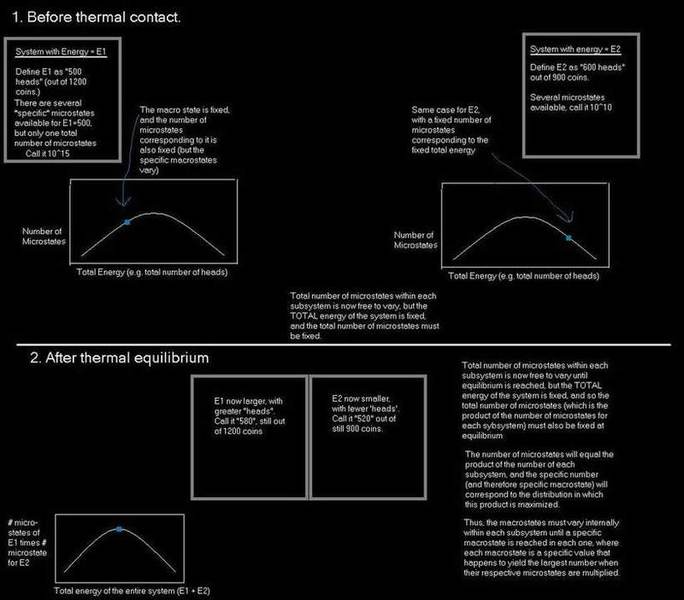
I'm trying to make sure I understand the basics of statistical mechanics and microstates/macrostates.
Being the nerd that I am, I have attempted to draw a diagram, as if I were explaining it to someone. If some one who is familiar with this topic could please review it and tell me if they see anything at all wrong, I would very much appreciate it.
The two systems are each two state systems, and to keep things simple I used the common "coin" analogy, where the total number of coins represents the total number of particles, and if they are "heads" then that means they are in the upper energy state. The two individual subsystems, as well as the final combined system, are all assumed to be completely closed. The only energy exchange allowed is between the two subsystems after they are in contact.