State the angles in terms of x , Circle theorems

In summary, the problem involves a circle with center O and diameter AB, and points C and D on the circle. We are asked to express the angles CAB and CBA in terms of x, where x is the measure of angle CDB. Using Thales theorem and the fact that ABDC is a cyclic quadrilateral, we can determine that $\angle CAB = 180-x$ and $\angle CBA = x-90$.
  • #1
mathlearn
331
0
Problem


View attachment 6048

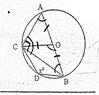
O is the center of the circle and AB is the diameter of this circle , C & D are points on this circle , If $\angle CDB=x^\circ$ ,State the following angles in terms of $x$

$\angle CAB$

$\angle CBA$

Workings & what is known

$OC=OB=OA$ radii of the same circle

$\therefore \angle {CBO} = \angle {OCB} = \angle {OAC} = \angle {OCA}$

$ACB=90^\circ$ Thales theorem

As $\angle BCO = \angle ACO $ it can be said that $\angle ACB$ is bisected

Many Thanks :)
 

Attachments

  • 003.jpg
    003.jpg
    14.2 KB · Views: 78
Mathematics news on Phys.org
  • #2
We are given that the quadrilateral $ABDC$ is cyclic, therefore:

\(\displaystyle x^{\circ}+\angle{CAB}=180^{\circ}\)

You are correct that $\angle{ACB}=90^{\circ}$

And so use:

\(\displaystyle \angle{CBA}+\angle{CAB}+\angle{ACB}=180^{\circ}\)
 
  • #3
MarkFL said:
We are given that the quadrilateral $ABDC$ is cyclic, therefore:

\(\displaystyle x^{\circ}+\angle{CAB}=180^{\circ}\)

You are correct that $\angle{ACB}=90^{\circ}$

And so use:

\(\displaystyle \angle{CBA}+\angle{CAB}+\angle{ACB}=180^{\circ}\)

Thanks :)

$\angle CAB+x=180$
$\angle CAB =180-x $

That's for $\angle CAB$ , Now For $\angle CBA$ as I think it is equal to $\angle CAO$ as in the figure $\angle CBA= 180-x$

Correct?

Many Thanks :)
 
  • #4
Using the sum of the interior angles of a triangle, I wrote:

\(\displaystyle \angle{CBA}+\angle{CAB}+\angle{ACB}=180^{\circ}\)

Now substitute:

\(\displaystyle \angle{CBA}+\left(180-x\right)^{\circ}+90^{\circ}=180^{\circ}\)

What do you get?
 
  • #5
MarkFL said:
Using the sum of the interior angles of a triangle, I wrote:

\(\displaystyle \angle{CBA}+\angle{CAB}+\angle{ACB}=180^{\circ}\)

Now substitute:

\(\displaystyle \angle{CBA}+\left(180-x\right)^{\circ}+90^{\circ}=180^{\circ}\)

What do you get?

Thanks :D , I get by substituting,

$\displaystyle \angle{CBA}+\left(180-x\right)^{\circ}+90^{\circ}=180^{\circ}$

$\displaystyle \angle{CBA}=x^{\circ} -90^{\circ}$

Correct ? :)

Many Thanks :)
 
  • #6
Yes, that's what I got as well. (Yes)
 
  • #7
MarkFL said:
Yes, that's what I got as well. (Yes)

Thank you very much MarkFL (Happy) (Smile) (Party)
 

FAQ: State the angles in terms of x , Circle theorems

What are the basic circle theorems?

The basic circle theorems include the angle at the centre being twice the angle at the circumference, angles in the same segment are equal, angles in a semicircle are right angles, and opposite angles in a cyclic quadrilateral add up to 180 degrees.

How do you state angles in terms of x in circle theorems?

To state angles in terms of x in circle theorems, you must first identify the angles that are related to x, such as angles in the same segment or angles in a cyclic quadrilateral. Then, you can use the given information and the circle theorems to set up equations and solve for x.

What is the angle at the centre theorem?

The angle at the centre theorem states that the angle at the centre of a circle is twice the angle at the circumference that subtends the same arc. In other words, if two angles, one at the centre and one at the circumference, have the same arc between them, the angle at the centre will be twice the size of the angle at the circumference.

What is the angle in a semicircle theorem?

The angle in a semicircle theorem states that any angle inscribed in a semicircle is a right angle. This means that the angle formed by a chord and the diameter of a circle (created by drawing a radius to each endpoint of the chord) is always a right angle.

How do you prove circle theorems?

To prove circle theorems, you must use the given information and the properties of circles to logically deduce the desired result. This may involve drawing additional lines or shapes, setting up equations, or using other theorems or properties. Some circle theorems may also require the use of algebra or geometry concepts to prove.

Similar threads

MHB State with reasons that angle ACB is bisected by line OC
Replies
9
Views
2K
Circle Theorems: Solving for Unknown Angles in Isosceles Triangles
Replies
6
Views
12K
Prove the ratio of AX:XB = 1:λ if X is a point on a circle
Replies
1
Views
2K

Hot Threads

Recent Insights

Back
Top