State the range of the reciprocal function?

[eleventhxhour]

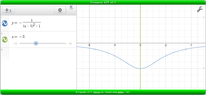
State the range of the reciprocal function of f(x) = - (x+3)^2 - 1.

I'm not sure if I did this right. I wrote that y is above/equal to -1 and below/equal to 0. Is this correct?

Also, how would you graph the reciprocal function of f(x) if there is no VA and only a HA?

 

[MarkFL]

We could write the reciprocal function $g$ as:

$$g(x)=\frac{1}{f(x)}=-\frac{1}{(x+3)^2+1}$$

Now, to find the rage of $g$, I would write:

$$y=-\frac{1}{(x+3)^2+1}=-\frac{1}{x^2+6x+10}$$

Now, express this equation in standard form as a quadratic in $x$, and then require the discriminant to be non-negative...this will result in an inequality which gives the range of the reciprocal function. You will find that you are correct.

To graph, consider that $g$ is the graph of $$y=-\frac{1}{x^2+1}$$, shifted 3 units to the left. This function is even, meaning it is symmetric about the $y$-axis, so $g$ will be symmetric across $x=-3$. It has as its maximum value that place where the denominator is the largest (because it is a negative reciprocal), which is the end-behavior, that is where x goes to $\pm\infty$. So, we know the $x$-axis is the horizontal asymptote. It has as its minimum value the place where the denominator is the smallest, that is, where the squared term is zero.

You now have enough information to construct a reasonably accurate graph. It should look like:

View attachment 3416